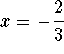. Consequently, the polynomial (x+2/3) divides evenly into
Using polynomial long division, we see that
How can we factor 
? Such a polynomial is called bi-quadratic. It can be solved by the following trick: we substitute 
to obtain
By the guessing method, we see that its factorization is given by:
Thus the roots are y=-1 and y=-2. But from this we can calculate the roots in terms of x; recall that .
Consequently the roots of the bi-quadratic polynomial are all complex: 
and 
.
Over the complex numbers, we can factor the polynomial as
Over the real numbers, the polynomials 
and 
are irreducible.
Thus the polynomial's factorization is:
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Helmut Knaust