

Find the solutions of the inequality
|2x-5|>x+1.
First we consider the case where
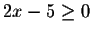 ,
i.e.
,
i.e.
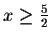 .
In this case
|2x-5|=2x-5, so we can write the inequality as
.
In this case
|2x-5|=2x-5, so we can write the inequality as
2x-5>x+1.
Subtracting x on both sides and adding 5, we get
x>6.
Now consider the case 2x-5< 0, i.e.
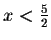 .
In this case
|2x-5|=-(2x-5)=5-2x, so we can write the inequality as
.
In this case
|2x-5|=-(2x-5)=5-2x, so we can write the inequality as
5-2x>x+1.
Adding 2x and subtracting 1 on both sides yields
4>3x,
so we obtain the requirement that
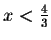 .
.
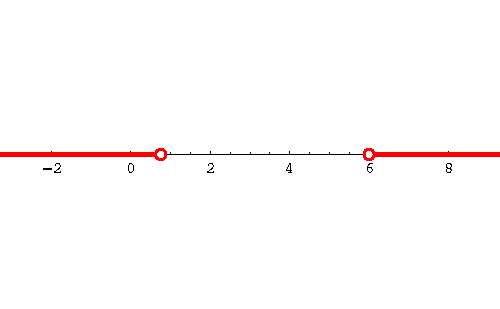
So a real number x is a solution of the original inequality if
or if
Thus the set of solutions is

[Back]
[Exercises]
[Next]
[Algebra]
[Trigonometry]
[Complex Variables]
[Calculus]
[Differential Equations]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Helmut Knaust
1998-06-08
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour



![]() ,
i.e.
,
i.e.
![]() .
In this case
|2x-5|=2x-5, so we can write the inequality as
.
In this case
|2x-5|=2x-5, so we can write the inequality as
![]() .
In this case
|2x-5|=-(2x-5)=5-2x, so we can write the inequality as
.
In this case
|2x-5|=-(2x-5)=5-2x, so we can write the inequality as

 S.O.S MATHematics home page
S.O.S MATHematics home page 