ON INVERSE FUNCTIONS
Composition of Functions
Suppose the rule of function f(x) is 
and the rule of function g(x) is 
. Suppose now that you want to "leapfrog" the functions as follows: Take a 2 in the domain of f and link it to 9 with the f(x) rule, and then take the 9 and link it to 157 with the g(x) rule. This is a lot of work and you would rather just work with one function, a function that would link the 2 directly to the 157.
Since the g function operates on f(x), we can write the composition as g(f(x)). Let's call the new function h(x) = g(f(x)). You can simplify from the inside out or the outside in.
Inside Out: 
It does.
Outside In: 
You can see that it is the same as the function we derived from the inside out.
The following is an example of finding the composition of three functions.
Example 4: Given three functions 
, 
, and 
,
Find the domain and range of each of the three functions.
The domain of the function f(x) is the set of all real numbers because f(x) is a polynomial. The range of the function f(x) is the set of all real numbers in the interval 
.
The domain of the function g(x) is the set of all real numbers greater than 8. The range of the function g(x) is the set of all real numbers greater than 0.
The domain of the function h(x) is the set of all real numbers 
. The range of the function h(x) is the set of all real numbers greater than or equal to 0.
Find the composite function f(g(h(x))).
The first step is to replace the h(x) with 
so that we have
.
Keep in mind that the composition of f with g does not make sense unless the quantity is a real number. Therefore, the first restriction on the domain of the composite function f(g(h(x)) is that x must belong to the set of real numbers defined as 
The second step is to replace the 
with 
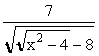so that we have
.
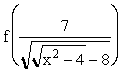Keep in mind that for the function f to work, the quantity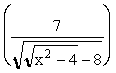 
has to be a real number. This means that 
. After you add 8 to both sides and square, the expression can be written 
. This means that the domain is now further restricted to the set of real numbers in the set 
The third step in the process is to replace 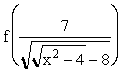with the expression 
.
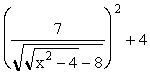The last expression can be simplified to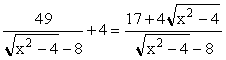 
and this last expression is the composite function f(g(h(x))).
What is the domain of the composite function f(g(h(x)))?
The domain of the composite function is the set of numbers common to the sets 
and . Therefore, the domain of the composite function is the set of real numbers in the interval .
Let’s check our answer with a number in the domain, say x = 10:
The function h(x) links the 10 to 
, the function g(x) links the to 5.22045253642…, and the function f(x) links the 5.22045253542… to 31.25311246746…. Let’s see if the new function will take us directly from 10 to 31.25311246746….
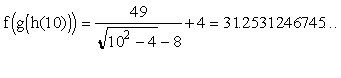
It does and our composite function is correct.
What would have happened if we tried to check our composite function with a number outside of the set of real numbers ?
Suppose we tried to check with the number x = 3:
The function h(x) links the 3 to 
, the function g(x) links the 
to Opps! An imaginary number. There is no link. This tells you that the number 3 is not in the domain of the composite function. You could have discovered the same thing if you graphed the composite function.
Recall that you can sometimes discern the domain of a function from its graph by noting where the graph exists. For example, if no part of the graph is located to the left of the y-axis, that means that no negative number is in the domain.
Review another example of finding the composition of functions.
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Author:Nancy Marcus