GRAPHS OF EXPONENTIAL FUNCTIONS GRAPHS OF EXPONENTIAL FUNCTIONS 
GRAPHS OF EXPONENTIAL FUNCTIONS
By Nancy Marcus
In this section we will illustrate, interpret, and discuss the graphs of exponential functions. We will also illustrate how you can use graphs to HELP you solve exponential problems. Recall that whenever there is a minus sign in front of the exponential term, it means that there is a reflection across the x-axis. Recall also that whenever there is a minus sign in front of the x in the exponent, it means that there is a reflection across the y-axis.
Horizontal and Vertical Shifts and Reflection Across the x-axis:
The following examples discuss the difference between the graph
of f(x) and the graph of -f(x + A) + B. Think of the sequence
of moves as 
. First, move the graph according to the directions
within the parenthesis: horizontally A units. If A is positive,
the move is to the left, if A is negative, the move is to the
right. Second, deal with the ( - 1) and reflect the graph about
the x-axis. Last, move the graph vertically B units. If B is
positive, the move is up. If B is negative the move is down.
Example 11: Graph the function
and the function
on the same
rectangular coordinate system. and answer the following questions
about each graph:
1.In what quadrants in the graph of the function
located?
In what quadrants is the graph of the function
located?
2.What is the x-intercept and the y-intercept on the graph of
the function
? What is the x-intercept and the y-intercept
on the graph of the function
?
3.Find the point (2, f(2)) on the graph of
and find (2, g(2))
on the graph of
. What do these two points have in common?
4.Describe the relationship between the two graphs.
5.How would you moved the graph of
so that it would be superimposed
on the graph of
? When you moved the graph, where would the
point (0, 1) on
be after the move?
|
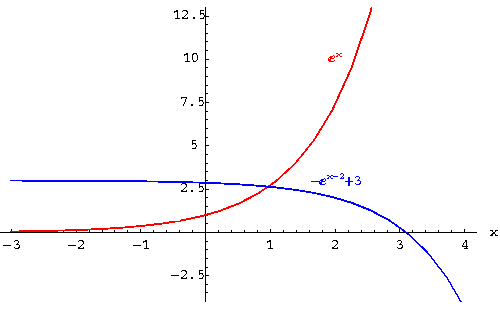
1.You can see that the first graph is located in quadrants I and II. The second graph is located in quadrants I, II, and IV. The graphs intersect in quadrant I.
2.There is no x-intercept for the f(x) graph because there is
no value of x for which 
equals zero. The x-intercept for the
g(x) graph is 2 + ln (3). Because .
3.The point 
is located on the graph of
. The point
is
located on the graph of
.
4.Both graphs have the same shape. It appears that the graph
of
is a result of shifting the graph of
to the right 2 units,
reflecting the graph across the x-axis, and then shifting the
graph upward 3 units.
After we moved the graph of
to the right 2 units, the point
(0, 1) on the original graph will be located at (2, 1). After
we reflect the graph over the x-axis, the point (2, 1) will be
moved to (2, -1). Finally, when we shift the graph upward 3
units, (2,-1) will be at (2, 2).
Example 12: Graph the function
and the function
on the same
rectangular coordinate system. and answer the following questions
about each graph:
1.In what quadrants in the graph of the function
located?
In what quadrants is the graph of the function
located?
2.What is the x-intercept and the y-intercept on the graph of
the function
? What is the x-intercept and the y-intercept
on the graph of the function
?
3.Find the point (2, f(2)) on the graph of
and find (2, g(2))
on the graph of
. What do these two points have in common?
4.Describe the relationship between the two graphs.
5.Describe how you would move the graph of
moved so that it would be superimposed on the graph of
. Where would the point (0, 1) on the graph of
wind up on after the move?
|
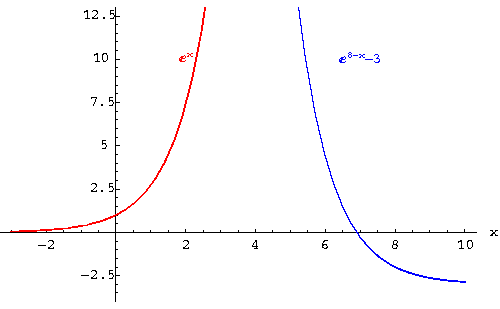
1.The graph of
is located in quadrants I and II. The graph
of
is located in quadrants I, and IV.
2.The graph of
does not cross the x-axis because there is
no value of x that would cause
to equal zero. The graph of
crosses the x-axis at 6.90138771133 because that is the solution
when we set 
:
3.The graph of
crosses the y-axis at 1, and the graph of
crosses the y-axis at 2,977.95798704 because
.
4.The point
is located on the graph of
. The point
is
located on the graph of
.
5.Both graphs have the same shape. The graph of
appears to
open in a direction opposite the direction of the graph of
and there appears to be some kind of horizontal and vertical
shift.
Whenever there is a minus in front of the x, it means there is a reflection across the y-axis. Whenever something is added or subtracted from the x in the exponent, it means there is a horizontal shift. Whenever a constant is added to the exponential term, it means there is a vertical shift.
6.Rewrite the equation
by factoring out a - 1 from the exponent to read 
.
From the equation, you can see that there is a reflection across the y-axis, a horizontal shift will be to the right 8 units, and a vertical shift down 3 units.
Let's try the translation from the point and see where we wind up. Reflect the point (2, 7.389) across the y-axis to (-2, 7.389). Now shift the point -2, 7.389) to the right 8 units to (6, 7.389), and finally shift the point (6, 7,389) down 3 units to (6, 4.389). How can you check whether you did this correctly. Evaluate g(6) and see if the answer is 4.389. If it is, you have correctly translated the graph.
Therefore, reflect the graph of
over the y-axis, shift (move) the reflected graph to the right 8 units and down 3 units. The
point (0, 1) would be moved to the right 8 units and down 3 units
to (0 + 8, 1 - 3) or (8, - 2).
If you would like to review another example, click on Example.
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Author: Nancy Marcus