 GRAPHS OF EXPONENTIAL FUNCTIONS
GRAPHS OF EXPONENTIAL FUNCTIONS  GRAPHS OF EXPONENTIAL FUNCTIONS
GRAPHS OF EXPONENTIAL FUNCTIONS 
GRAPHS OF EXPONENTIAL FUNCTIONS
By Nancy Marcus
In this section we will illustrate, interpret, and discuss the graphs of exponential functions. We will also illustrate how you can use graphs to HELP you solve exponential problems.
Stretch and Shrink: The following examples discuss the difference between the graph of f(x) and f(Cx).
Example 15: Graph the function
![]() and the function
and the function
![]() on the same
rectangular coordinate system. and answer the following questions
about each graph:
on the same
rectangular coordinate system. and answer the following questions
about each graph:
1.In what quadrants in the graph of the function ![]() located? In what quadrants is the graph of the function .
located?
located? In what quadrants is the graph of the function .
located?
2.What is the x-intercept and the y-intercept on the graph of
the function ![]() ? What is the x-intercept and the y-intercept
on the graph of the function
? What is the x-intercept and the y-intercept
on the graph of the function ![]() ?
?
3.Find the point (2, f(2)) on the graph of ![]() and find (2, g(2)) on the graph of
and find (2, g(2)) on the graph of ![]() . What do these two points have in common?
. What do these two points have in common?
4.Describe the relationship between the two graphs.
5.Write g(x) in terms of f(x).
6.How would you moved the graph of ![]() so that it would be superimposed on the graph of
so that it would be superimposed on the graph of ![]() ? When you moved the graph, where would the point (0, 1) on
? When you moved the graph, where would the point (0, 1) on ![]() be after the move?
be after the move?

|
1.You can see that the both graphs are located in quadrants I and II.
2.You can see that neither of the graphs crosses the x-axis;
therefore, neither of the graphs has an x-intercept. Notice
that both graphs cross the y-axis at 1 because ![]() .
.
3.The point ![]() is located on the graph of
is located on the graph of ![]() . The point
. The point ![]() is
located on the graph of
is
located on the graph of ![]() . This is a significant stretch.
. This is a significant stretch.
4.Even though the graph of g(x) looks difference from the graph of f(x), both graphs have the same shape. The graph of g(x) is located above the graph of f(x) for all positive values of x, and the graph of g(x) is located below the graph of f(x) for all negative values of x. Both graphs cross the y-axis at the same point.
The graph of
is a result of stretching and shrinking the graph
of ![]() . For example, for every positive value of x the value
of g(x) is larger than the value of f(x). For every negative
value of x, just the opposite is true. When the value of x is
0, both functions values are the same.
. For example, for every positive value of x the value
of g(x) is larger than the value of f(x). For every negative
value of x, just the opposite is true. When the value of x is
0, both functions values are the same.
5. ![]() =
= ![]()
6.The point (0, 1) on the graph of ![]() does not move. The point (5, 148.4) would be stretched to (5, 3,269). The point (-3,
0.05) would be shrunk to (-3, 0.0000003).
does not move. The point (5, 148.4) would be stretched to (5, 3,269). The point (-3,
0.05) would be shrunk to (-3, 0.0000003).
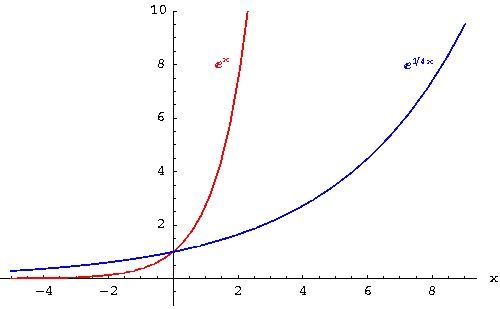
Example 16: Graph the function
![]() and the function
and the function
![]() on the same
rectangular coordinate system. and answer the following questions
about each graph:
on the same
rectangular coordinate system. and answer the following questions
about each graph:
1.In what quadrants in the graph of the function ![]() located? In what quadrants is the graph of the function located?
located? In what quadrants is the graph of the function located?
2.What is the x-intercept and the y-intercept on the graph of
the function ![]() ? What is the x-intercept and the y-intercept
on the graph of the function
? What is the x-intercept and the y-intercept
on the graph of the function ![]() ?
?
3.Find the point (2, f(2)) on the graph of ![]() and find (2, g(2)) on the graph of
and find (2, g(2)) on the graph of ![]() . What do these two points have in common?
. What do these two points have in common?
4.Describe the relationship between the two graphs.
5.Write g(x) in terms of f(x).
6.Describe how you would move the graph of ![]() moved so that it would be superimposed on the graph of
moved so that it would be superimposed on the graph of ![]() . Where would the point (0, 1) on the graph of
. Where would the point (0, 1) on the graph of ![]() wind up on after the move?
wind up on after the move?
|
1.Both graphs are located in quadrants I and II. This means that the function values for both functions will always be positive.
Neither of the graphs cross the x-axis. This means that there is no value of x that will cause the function value to be zero.
2.Both graphs cross the y-axis at y = 1.
3.The point ![]() is located on the graph of
is located on the graph of ![]() . The point
. The point ![]() is
located on the graph of
is
located on the graph of ![]() .
.
4.Both graphs have the same shape. The graph of g(x) is located below the graph of f(x) in the first quadrant (for all positive values of x), and the graph of g(x) is located above the graph of f(x) in the second quadrant (for all negative values of x).
5. ![]() =
= ![]()
6.=.The point (0, 1) would stay in the same place. The point (1, 2.718282) on the graph of f(x) would be moved to (1, 1.284025). The point ( -1, 0.367879) would be moved to (-1, 0.778801).
If you would like to review another example, click on Example.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus