 GRAPHS OF LOGARITHMIC FUNCTIONS
GRAPHS OF LOGARITHMIC FUNCTIONS

In this section we will illustrate, interpret, and discuss the graphs of logarithmic functions.
Stretch and Shrink: The following examples discuss the difference between the graph of f(x) and the graph of Cf(x):
Example 13:
Graph the function 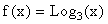 and the function
and the function 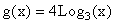 on the same rectangular coordinate system. Recall that you will have to convert the above functions to either the natural log or log with base 10 to graph them on your calculator. The function
on the same rectangular coordinate system. Recall that you will have to convert the above functions to either the natural log or log with base 10 to graph them on your calculator. The function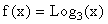 can be written as
can be written as  and the function
and the function 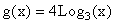 can be written as
can be written as 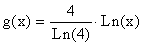 for graphing purposes. Answer the following questions about each graph:
for graphing purposes. Answer the following questions about each graph:
- In what quadrants in the graph of the function
 located? In what quadrants is the graph of the function
located? In what quadrants is the graph of the function 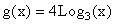 located?
located?
- State the domain of each function.
- What is the x-intercept and the y-intercept on the graph of the function
 ? What is the x-intercept and the y-intercept on the graph of the function
? What is the x-intercept and the y-intercept on the graph of the function 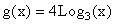 ?
?
- Find the point (2, f(2)) on the graph of
 and find (2, g(2)) on the graph of
and find (2, g(2)) on the graph of 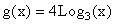 . What do these two points have in common?
. What do these two points have in common?
- Describe the relationship between the two graphs.
- How would you moved the graph of
 so that it would be superimposed on the graph of
so that it would be superimposed on the graph of 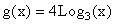 ? When you moved the graph, where would the point (9, 2) on
? When you moved the graph, where would the point (9, 2) on  be after the move?
be after the move?
- You can see that the both graphs are located in quadrants I and IV.
- The domain of both functions is the set of positive real numbers.
- You can see that neither of the graphs crosses the y-axis; therefore, neither of the graphs has a y-intercept. Notice that both graphs cross the x-axis at 1 because
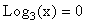 when x = 1 and
when x = 1 and  when x = 1. The y-coordinate of g(x) is 4 times the y-coordinate of f(x).
when x = 1. The y-coordinate of g(x) is 4 times the y-coordinate of f(x).
- The point
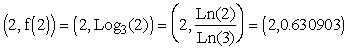 is located on the graph of
is located on the graph of  . The point
. The point 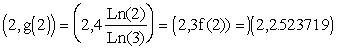 is located on the graph of
is located on the graph of 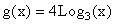 .
.
- Both graphs have the basic shape shared by all logarithmic functions. It appears that the graph of
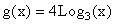 is a result of stretching the graph of
is a result of stretching the graph of  . For example, for every value of x the value of g(x) is 4 times larger than the value of f(x).
. For example, for every value of x the value of g(x) is 4 times larger than the value of f(x).
- The graph f(x) is stretched up to be superimposed on the graph of g(x). The point (9, 2) on the graph of
 would be moved up to (9,8) because every function value of g(x) is 4 times the function value of f(x). If (a, b) were a point on the graph of f(x), then the point (a, 4b) would be a point on the graph of g(x).
would be moved up to (9,8) because every function value of g(x) is 4 times the function value of f(x). If (a, b) were a point on the graph of f(x), then the point (a, 4b) would be a point on the graph of g(x).
Example 14:
Graph the function 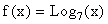 and the function
and the function 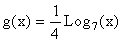 on the same rectangular coordinate system. Recall that you will have to convert the above functions to either the natural log or log with base 10 to graph them on your calculator. The function
on the same rectangular coordinate system. Recall that you will have to convert the above functions to either the natural log or log with base 10 to graph them on your calculator. The function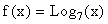 can be written as
can be written as 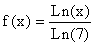 and the function
and the function 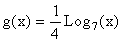 can be written as
can be written as 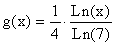 for graphing purposes. Answer the following questions about each graph:
for graphing purposes. Answer the following questions about each graph:
- In what quadrants in the graph of the function
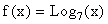 located? In what quadrants is the graph of the function
located? In what quadrants is the graph of the function 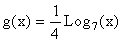 located?
located?
- State the domain of each function.
- What is the x-intercept and the y-intercept on the graph of the function
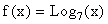 ? What is the x-intercept and the y-intercept on the graph of the function
? What is the x-intercept and the y-intercept on the graph of the function 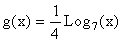 ?
?
- Find the point (49, f(49)) on the graph of
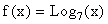 and find (49, g(49)) on the graph of
and find (49, g(49)) on the graph of 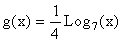 . What do these two points have in common?
. What do these two points have in common?
- Describe the relationship between the two graphs.
- Describe how you would move the graph of
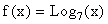 moved so that it would be superimposed on the graph of . Where would the point (343, 3) on the graph of
moved so that it would be superimposed on the graph of . Where would the point (343, 3) on the graph of 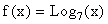 wind up on after the move?
wind up on after the move?
- Both graphs are located in quadrants I and IV.
- The domain of both functions is the set of positive real numbers.
- Neither graph crosses the y-axis; therefore, there are no y-intercepts. The graph of
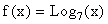 crosses the x-axis at 1, and the graph of
crosses the x-axis at 1, and the graph of 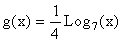 crosses the x-axis at 1.
crosses the x-axis at 1.
- The point
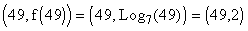 is located on the graph of
is located on the graph of 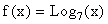 . The point
. The point 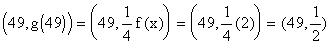 is located on the graph of
is located on the graph of 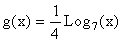 . For each x-coordinate, the y-coordinate of g(x) is
. For each x-coordinate, the y-coordinate of g(x) is 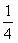 of the y-coordinate of f(x).
of the y-coordinate of f(x).
- Both graphs have the same shape. The graph of
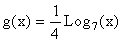 appears to shrink. It is like you just let the graph of f(x) kind of slip down a little to be superimposed upon the graph of g(x)..
appears to shrink. It is like you just let the graph of f(x) kind of slip down a little to be superimposed upon the graph of g(x)..
- Notice that the graph of g(x) is below the graph of f(x). This is because for every value of x, the value of g(x) is
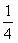 the value of f(x). The point (343,3) on f(x) would
the value of f(x). The point (343,3) on f(x) would
be shifted to 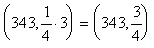 on g(x)
on g(x)
If you would like to review another example, click on Example.

[Exponential Rules]
[Logarithms]
[Algebra]
[Trigonometry ]
[Complex Variables]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Author: Nancy
Marcus
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 GRAPHS OF LOGARITHMIC FUNCTIONS
GRAPHS OF LOGARITHMIC FUNCTIONS  GRAPHS OF LOGARITHMIC FUNCTIONS
GRAPHS OF LOGARITHMIC FUNCTIONS 
![]() and the function
and the function ![]() on the same rectangular coordinate system. Recall that you will have to convert the above functions to either the natural log or log with base 10 to graph them on your calculator. The function
on the same rectangular coordinate system. Recall that you will have to convert the above functions to either the natural log or log with base 10 to graph them on your calculator. The function![]() can be written as
can be written as ![]() and the function
and the function ![]() can be written as
can be written as ![]() for graphing purposes. Answer the following questions about each graph:
for graphing purposes. Answer the following questions about each graph: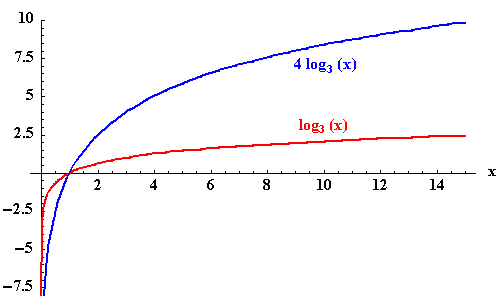
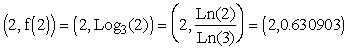 is located on the graph of
is located on the graph of 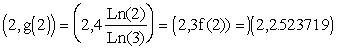 is located on the graph of
is located on the graph of ![]() and the function
and the function ![]() on the same rectangular coordinate system. Recall that you will have to convert the above functions to either the natural log or log with base 10 to graph them on your calculator. The function
on the same rectangular coordinate system. Recall that you will have to convert the above functions to either the natural log or log with base 10 to graph them on your calculator. The function![]() can be written as
can be written as ![]() and the function
and the function ![]() can be written as
can be written as ![]() for graphing purposes. Answer the following questions about each graph:
for graphing purposes. Answer the following questions about each graph: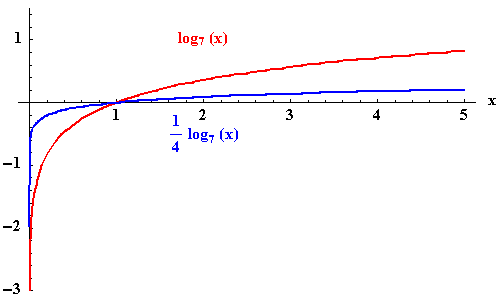
![]() on g(x)
on g(x)
 S.O.S MATHematics home page
S.O.S MATHematics home page 