 CHANGING THE BASE OF A LOGARITHM - Example
CHANGING THE BASE OF A LOGARITHM - Example CHANGING THE BASE OF A LOGARITHM - Example
CHANGING THE BASE OF A LOGARITHM - Example
Let a, b, and x be positive real numbers such that neither a nor b equals 1.
Then ![]() can be converted to the base b by the formula
can be converted to the base b by the formula ![]() . Let's verify this with the following example.
. Let's verify this with the following example.

Example 1: Find ![]() .
.
Answer 1: -36.158608
Solution: Convert to the base 10.
![]()
Check: Let's check the answer. If 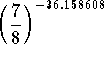 equals 125, we have worked the problem correctly.
equals 125, we have worked the problem correctly. 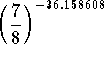 = 124.999443. Close enough. The reason the check
does not come out exactly is that we rounded the log125, the
= 124.999443. Close enough. The reason the check
does not come out exactly is that we rounded the log125, the ![]() , and the quotient of the two logs. If you use continuous calculations
on your calculator, the answer will be closer to 125.
, and the quotient of the two logs. If you use continuous calculations
on your calculator, the answer will be closer to 125.
Solution 2: You can also work this problem using natural logarithms. Convert
![]() to the base e.
to the base e.
![]()
Check: Let's check the answer. If 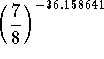 equals 125, we have worked the problem correctly.
equals 125, we have worked the problem correctly. 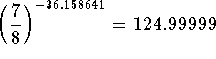 . Close enough. The reason the check
does not come out exactly is that we rounded the ln125, the
. Close enough. The reason the check
does not come out exactly is that we rounded the ln125, the ![]() , and the quotient of the two logs. If you use continuous calculations on
your calculator, the answer will be closer to 125.
, and the quotient of the two logs. If you use continuous calculations on
your calculator, the answer will be closer to 125.
If you would like to review another example of changing the base of a logarithm, click on Example.

 S.O.S MATHematics home page
S.O.S MATHematics home pageDo you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus