 RULES OF LOGARITHMS - Example
RULES OF LOGARITHMS - Example
 RULES OF LOGARITHMS - Example
RULES OF LOGARITHMS - Example 
Let a be a positive number such that a does not equal 1, let
n be a real number, and let u and v be positive real numbers.
Logarithmic Rule 2:
![]()

Example 5: Expand 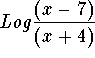 and state the domain.
and state the domain.
Solution: The domain of 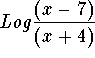 is the set of all real numbers such that
is the set of all real numbers such that
![]()
Either x-7>0 and x+4>0 or x-7<0 and x+4<0 .
This means that if x > 7 and x > - 4, both the numerator and the
denominators are positive and the value of the fraction is positive. If we
restrict the values of x to be greater than 7, they are automatically
greater than - 4 and the domain can be simplified to x > 7.
or
This means that if x > 7 and x < -4, both the numerator and the denominator are negative, and the value of the fraction is positive. If we restrict the values of x to be less than - 4, they are automatically less than 7, and the domain can be simplified to x < -4.
The domain of 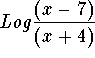 is the set of all real numbers that are in the interval
is the set of all real numbers that are in the interval ![]() or
or ![]() , that is
, that is
![]()
The domain of ![]() is the set of
real numbers that works for both. The real number x > 7 works for the
first term and the real number x > -4 works for the second term. You need a set of numbers that will work for both terms. The domain is the set of real numbers where x > 7.
is the set of
real numbers that works for both. The real number x > 7 works for the
first term and the real number x > -4 works for the second term. You need a set of numbers that will work for both terms. The domain is the set of real numbers where x > 7.
Therefore, 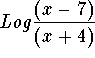 is equivalent to
is equivalent to ![]() only when the domain is restricted to those real numbers x > 7.
only when the domain is restricted to those real numbers x > 7.
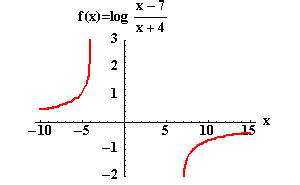
| 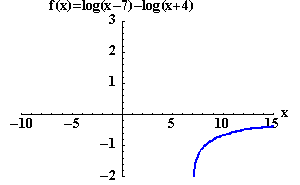
|
If you would like to review another example, click on Example.

 S.O.S.
MATHematics home page
S.O.S.
MATHematics home pageDo you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus