RULES OF LOGARITHMS - Example

Let a be a positive number such that a does not equal 1, let n be a real number, and let u and v be positive real numbers.

Logarithmic Rule 2:

Example 6: Expand 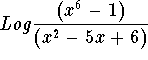and state the domain.

Solution: The domain of 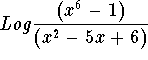is the set of all real numbers such that

You can find the domain algebraically as we did in the previous examples or you can graph

and notice for what values of x is the graph located above the x-axis. The graph rises above the x-axis to the left of - 1 and to the right of + 1. Therefore the domain of the initial expression is the set of real numbers x such that x < - 1 or x > + 1.
The expression 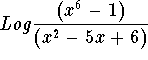can be simplified to

The expression

and this can be written as

as long as each term is valid.
For to be valid, we must have x > 1. For to be valid, we must have x> - 1. Both terms and are always valid because the expressions and are always positive. Therefore, if we restrict the domain to all real numbers greater than 1, the expansion of is valid.

The expression can be simplified to

The expression can be written as as long as each term is valid.
For to be valid, we must have x > 2. For to be valid, we must have x > 3. Both terms are valid when x > 3. Therefore, if we restrict the domain to all real numbers greater than 3, the expansion of is valid.

And we can say that

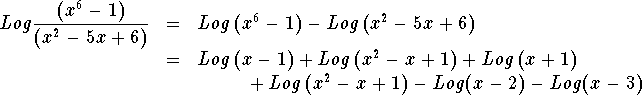
as long as we restrict the domain to the set of real numbers greater than 3.

Check: Pick any number in the domain, say x = 10. Find the value of the original expression when x = 10. The value of the original expression 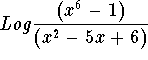when x = 10 is

The value of the final expression

when x = 10 is

Since both values are the same when x = 10, the original expression and the final expression are equivalent at x = 10. We can also say that for all values of x greater than 3, the original expression is equivalent to the final expression.

If you would like to work a problem, click on Problem.

S.O.S. MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.