 LOGARITHMS AND THEIR INVERSES
LOGARITHMS AND THEIR INVERSES  LOGARITHMS AND THEIR INVERSES
LOGARITHMS AND THEIR INVERSES 
If the logarithmic function is one-to-one,
its inverse exits. The inverse of a logarithmic function is
an exponential function. When you graph both the logarithmic
function and its inverse, and you also graph the line y = x,
you will note that the graphs of the logarithmic function and
the exponential function are mirror images of one another with
respect to the line y = x. If you were to fold the graph along
the line y = x and hold the paper up to a light, you would note
that the two graphs are superimposed on one another. Another
way of saying this is that a logarithmic function and its inverse
are symmetrical with respect to the line y = x.
Problem 3: Find the inverse, if it exists, to the function
![]()
If it does not exist, indicate the restrict domain where it will exist
and find the inverse over the restricted domain..
Solution: By inspection of the graph of f(x), you can tell the
domain consists of all real numbers to the right of ![]() . You know also that you can only take the log of a
positive number, so when you solve 4x-7>0, x must be a real number
greater than
. You know also that you can only take the log of a
positive number, so when you solve 4x-7>0, x must be a real number
greater than ![]() .
.
You can tell that the function is one-to-one and therefore has an
inverse. How can you tell from the graph that f(x) is a one-to-one
function? You use the horizontal line test. Run a horizontal line
across the graph; if it intersects the graph more than once at any
given time, it is not one-to-one. Since the inverse exists, you know
that its range is equal to the domain of f(x), or all real numbers
greater than ![]() .
.
You know that
![]()
We have to isolate the ![]() in the equation
in the equation
![]()
![]()
![]()
![]()
![]()
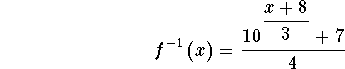
![]()
This means that the point (10, -3.44445818036) is located on the graph
of f(x).
If we can show that the point (-3.44445818036, 10) is located
on the graph of the inverse, we have illustrated that we have
calculated the inverse correctly, at least for these points.
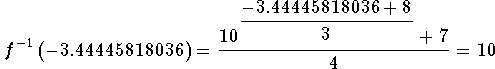
You have correctly worked the problem.
If you would like to go back to the menu, click on menu below.

 S.O.S MATHematics home page
S.O.S MATHematics home pageDo you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus