 PROPERTIES OF LOGARITHMS
PROPERTIES OF LOGARITHMS

SOLVING LOGARITHMIC EQUATIONS
1. To solve a logarithmic equation, rewrite the equation in exponential form and solve for the variable.
Example 6: Solve for x in the equation
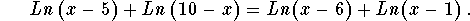
Solution:
-
- Step 1: The term Ln(x-5) is valid when x>5, the term Ln(10-x) is valid when x<10, the term Ln(x-6) is valid when x>6, and the term Ln(x-1) is valid when x>1. If we restrict the domain to the set of all real numbers x between 6 and
10 or 6<x<10, every term in the equation is valid.
Graph the function
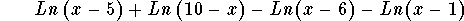
[formed by subtracting right side of original problem from the left
side of equation]
and note that the entire graph is located between the values of x = 6 and x = 10.
Note also that the graph crosses the x-axis at 7. This means that the
solution to the problem is 7.
-
- Step 2: Simplify both sides of the original equation by combining the logarithmic terms according to Logarithmic Rule 1:
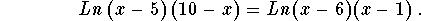
-
- Step 3: The above equation has the same form as the equation Ln(a) = Ln(b). The a must equal the b for the equation to be valid. Therefore,
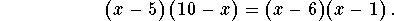
-
- Step 4: Expand each side of the above equation:
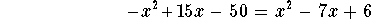
-
- Step 5: Add
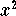 to both sides:
to both sides:
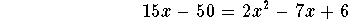
-
- Step 6: Subtract 15x from both sides of the above equation:
-
- Step 7: Add 50 to both sides of the above equation:
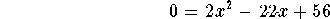
-
- Step 8: Divide both sides of the above equation by 2:

-
- Step 9: Solve for x using the quadratic formula:
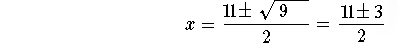
x=7,4. Only 7 is in the interval (6,10).
If you would like to review another example, click on Example.

[Back to Rules of Logarithms]
[Back to Exponential Functions]
[Algebra]
[Trigonometry]
[Complex
Variables]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Author: Nancy
Marcus
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 PROPERTIES OF LOGARITHMS
PROPERTIES OF LOGARITHMS PROPERTIES OF LOGARITHMS
PROPERTIES OF LOGARITHMS
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

 S.O.S MATHematics home page
S.O.S MATHematics home page