 PROPERTIES OF LOGARITHMS
PROPERTIES OF LOGARITHMS PROPERTIES OF LOGARITHMS
PROPERTIES OF LOGARITHMS
1. To solve a logarithmic equation, rewrite the equation in exponential form and solve for the variable.
Example 8: If ![]() , and a and b are positive, show that
, and a and b are positive, show that
![]()
no matter what positive value for the base is used for the logarithms (but
it is understood that the same base is used throughout).
Solution:
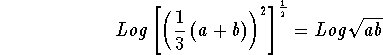
All we did to the quantity with the brackets on the left side of the
equation is raise it to a net power of 1. ![]() Remember that
Remember that 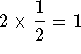
![]() . All we did to the right side was simplify it using Logarithm Rules 1 and 3.
. All we did to the right side was simplify it using Logarithm Rules 1 and 3.
![]()
![]()
![]()
or ![]() .
.
![]()
can be simplified using Logarithmic Rules 1 and 3:
![]()
If you would like to review another example, click on Example.

 S.O.S MATHematics home page
S.O.S MATHematics home pageDo you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus