 PROPERTIES OF LOGARITHMS
PROPERTIES OF LOGARITHMS PROPERTIES OF LOGARITHMS
PROPERTIES OF LOGARITHMS
1. To solve a logarithmic equation, rewrite the equation in exponential form and solve for the variable.
Example 9: Solve for x (assuming a>b>0) in the equation
![]()
Solution:
![]()
![]()
![]()
![]()
![]()
or
![]()
![]()
which yields
![]()
or
![]()
Answer: 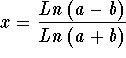
Check: Let's check our answer using a=9 and b=5. You can check your answer with any positive values of a and b as long as the value of a is greater than the value of b (initial restriction).
If a = 9 and b = 5, then
![]()
When the values for a, b, and x are substituted in the left side of the initial equation, the value is as follows:
![]()
When the values for a, b, and x are substituted in the right side of the initial equation, the value is as follows:
![]()
The answer checks for these values of a and b.
If you would like to work on problems, click on Problems.

 S.O.S MATHematics home page
S.O.S MATHematics home pageDo you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus