 APPLICATIONS OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS
APPLICATIONS OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS

APPLICATIONS OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS
(Interest Rate Word Problems)
1. To solve an exponential or logarithmic word problems, convert the narrative to an equation and solve the equation.
Problem 3: If you invested $1,000 in an account paying an annual
percentage rate (quoted rate) compound daily (based on a bank
year of 360 days) and you wanted to have $2,500 in your account
at the end of your investment time, what interest rate would
you need if the investment time were 1 year, 10 years, 20 years,
100 years?
Answer: 1 year = 91.75%, 10 years = 9.16%, 20 years = 4.58%,
and 100 years 0.92%
Solution and Explanations:
Use the formula
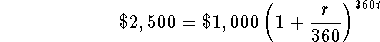
where $2,500 is the balance at the end of a certain time period,
$1,000 is the beginning investment, t is the number of years, and r
is the annual percentage rate. The annual rate of r% is converted to
a daily interest rate since the compounding is daily (360 times per
year). Take the annual interest rate of 4% and divide by 360 to
obtain the daily interest rate. The exponent is 360t because there
are 360 compounding periods in every year. Therefore, 360t represents
the number of compounding periods during t years.
To find the rate for 1 year:
-
- Step 1: Substitute 1 for t in the equation
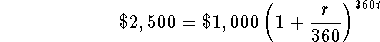
to derive r:
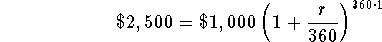
-
- Step 2: Divide both sides of the above equation by $1,000:
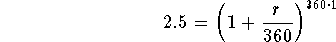
-
- Step 3: Take the natural logarithm of both sides of the above
equation:
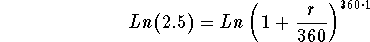
-
- Step 4: Simplify the right side of the above equation using the
third rule of logarithms:
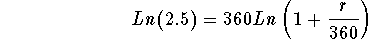
-
- Step 5: Divide both sides of the above equation by 360:
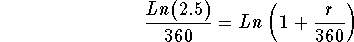
-
- Step 6: Simplify the left side of the above equation:
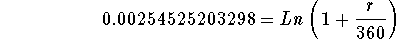
-
- Step 7: Convert the above equation to an exponential equation
with base e and exponent 0.00254525203298:
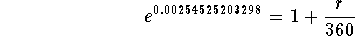
-
- Step 8: Simplify the left side of the above equation:
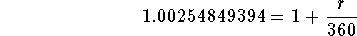
-
- Step 9: Subtract 1 from both sides of the above equation:
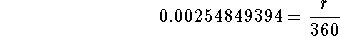
-
- Step 10: Multiply both sides of the above equation by 360:

This means the interest rate would have to be 91.75% (rounded) for the year.
-
- Check:
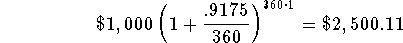
This is a close enough check. Remember it will not check perfectly
before we rounded the interest rate.
To find the rate for 10 year:
-
- Step 1: Substitute 10 for t in the equation
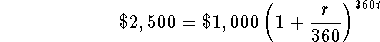
to derive r:
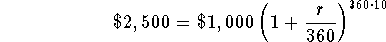
-
- Step 2: Divide both sides of the above equation by $1,000:
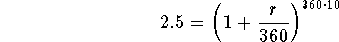
-
- Step 3: Take the natural logarithm of both sides of the above
equation:
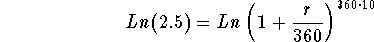
-
- Step 4: Simplify the right side of the above equation using the
third rule of logarithms:
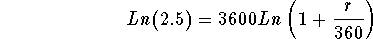
-
- Step 5: Divide both sides of the above equation by 3600:
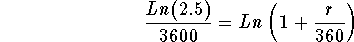
-
- Step 6: Simplify the left side of the above equation:
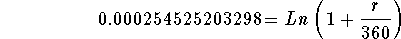
-
- Step 7: Convert the above equation to an exponential equation
with base e and exponent 0.000254525203298:
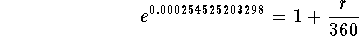
-
- Step 8: Simplify the left side of the above equation:
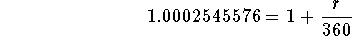
-
- Step 9: Subtract 1 from both sides of the above equation:
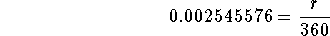
-
- Step 10: Multiply both sides of the above equation by 360:

This means the interest rate would have to be 9.16% (rounded) per
year for 10 years.
-
- Check:
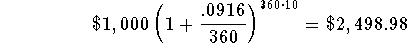
This is a close enough check. Remember it will not check perfectly
before we rounded the interest rate.
To find the rate for 20 year:
-
- Step 1: Substitute 20 for t in the equation
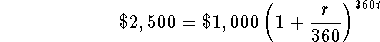
to derive r:
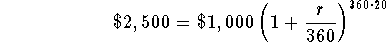
-
- Step 2: Divide both sides of the above equation by $1,000:
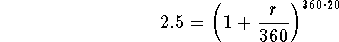
-
- Step 3: Take the natural logarithm of both sides of the above
equation:
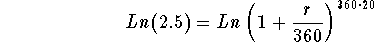
-
- Step 4: Simplify the right side of the above equation using the
third rule of logarithms:
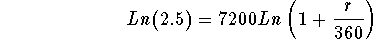
-
- Step 5: Divide both sides of the above equation by 7200:
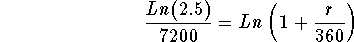
-
- Step 6: Simplify the left side of the above equation:
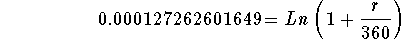
-
- Step 7: Convert the above equation to an exponential equation
with base e and exponent 0.000127262601649:
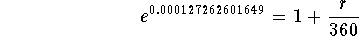
-
- Step 8: Simplify the left side of the above equation:
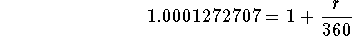
-
- Step 9: Subtract 1 from both sides of the above equation:
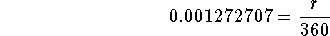
-
- Step 10: Multiply both sides of the above equation by 360:

This means the interest rate would have to be 4.58% (rounded) per
year for 20 years.
-
- Check:
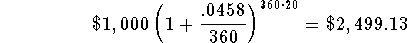
This is a close enough check. Remember it will not check perfectly
before we rounded the interest rate.
To find the rate for 100 year:
-
- Step 1: Substitute 100 for t in the equation
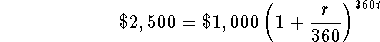
to derive r:
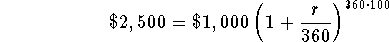
-
- Step 2: Divide both sides of the above equation by $1,000:
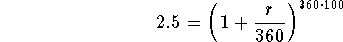
-
- Step 3: Take the natural logarithm of both sides of the above
equation:
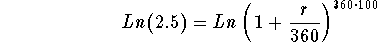
-
- Step 4: Simplify the right side of the above equation using the
third rule of logarithms:
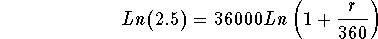
-
- Step 5: Divide both sides of the above equation by 36000:
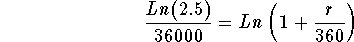
-
- Step 6: Simplify the left side of the above equation:
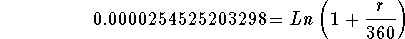
-
- Step 7: Convert the above equation to an exponential equation
with base e and exponent 0.0000254525203298:
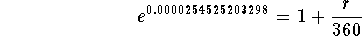
-
- Step 8: Simplify the left side of the above equation:
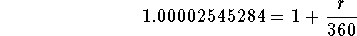
-
- Step 9: Subtract 1 from both sides of the above equation:
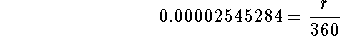
-
- Step 10: Multiply both sides of the above equation by 360:

This means the interest rate would have to be 0.92% (rounded) per
year for 100 years.
-
- Check:
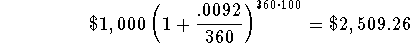
This is a close enough check. Remember it will not check perfectly
before we rounded the interest rate.
If you would like to work another problem and check the answer
and solution, click on Problem.

[Previous Problem]
[Next Problem]
[Menu Back to Rule 3]
[Algebra]
[Trigonometry]
[Complex
Variables]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Author: Nancy
Marcus
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 APPLICATIONS OF EXPONENTIAL AND
APPLICATIONS OF EXPONENTIAL AND  APPLICATIONS OF EXPONENTIAL AND
APPLICATIONS OF EXPONENTIAL AND 
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

 S.O.S MATHematics home page
S.O.S MATHematics home page