APPLICATIONS OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS

To solve an exponential or logarithmic word problem, convert the narrative to an equation and solve the equation.
There is a relationship between the mortgage amount, the number of payments, the amount of the payment, how often the payment is made, and the interest rate. The following formulas illustrate the relationship:

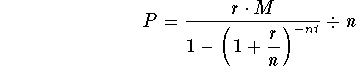
where P = the payment, r = the annual rate, M = the mortgage amount, t = the number of years, and n = the number of payments per year.

Example 1: What is the monthly payment on a mortgage of $75,000 with an 8% interest rate that runs for 20 years, 25 years, 30 years? How much interest is paid over 20 years, 25 years, 30 years?

Answer: 20 years: payment = $627.33 per month; after 20 years of payments, you will have paid $150,559.20 ($75,559.20 in interest)
25 years: payment = $578.86 per month; after 25 years of payments, you will have paid $173,658.00 ($98,658.00 in interest).
30 years payment = $$550.32 per month; after 30 years of payments, you will have paid $198,116.43 ($123,116.43 in interest).

Solution and Explanations:

20 Years: In the equation

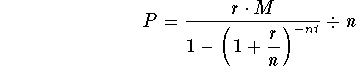
substitute $75,000 for M (the mortgage amount), 8% for r (the annual interest rate), 20 for t (the number of years), and 12 for n (the number of payments per year. You are solving for P (the monthly payment for the 20 years)

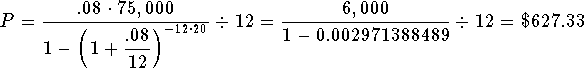
The monthly payment will be $627.33. After 20 years of payments, you will have paid

Everything over the initial $75,000 is interest. Therefore, after 20 years, you will have paid

in interest.

25 Years: In the equation

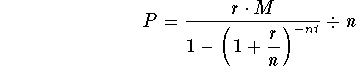
substitute $75,000 for M (the mortgage amount), 8% for r (the annual interest rate), 25 for t (the number of years), and 12 for n (the number of payments per year. You are solving for P (the monthly payment for the 25 years)

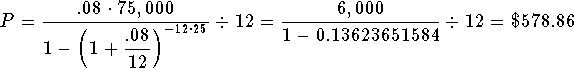
The monthly payment will be $578.86. After 25 years of payments, you will have paid

Everything over the initial $75,000 is interest. Therefore, after 25 years, you will have paid

in interest.

30 Years: In the equation

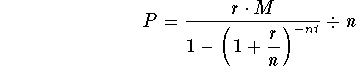
substitute $75,000 for M (the mortgage amount), 8% for r (the annual interest rate), 30 for t (the number of years), and 12 for n (the number of payments per year. You are solving for P (the monthly payment for the 30 years)

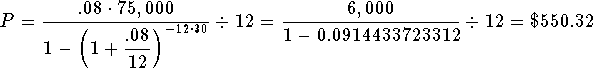
The monthly payment will be $550.32. After 30 years of payments, you will have paid

Everything over the initial $75,000 is interest. Everything over the initial $75,000 is interest. Therefore, after 30 years, you will have paid

in interest.

If you would like to review another example, click on Example.

Work the following problems. If you want to check your answer and solution click on Answer.

Problem 1: Find the monthly payments on a $100,000, 30-year mortgage, with monthly payments at 9.5%. How much interest will you have over the 30 years?

Answer

Problem 2: Suppose you wanted to take out a mortgage for $100,000 with monthly payments at 9%, but you could only afford $800 per month payments. How long would you have to make payments to pay off the mortgage, and how much interest would you pay for this payment period?

Answer

Problem 3: Suppose a bank offers you a 10% interest rate on a 20-year mortgage to be paid back with monthly payments. Suppose the most you can afford to pay in monthly payments is $700. How much of a mortgage could you afford?

Answer

Problem 4: Suppose you need to take out a mortgage of $100,000. All you can afford for monthly payments is $800. You will retire in 25 years; therefore, the longest you can make these payments is 25 years. What interest rate would you need to take out a mortgage of $100,000 and pay it back in 300 monthly payments of $800

Answer

[Back to Solving Word Problems] [Exponential Rules] [Logarithms]

[Algebra] [Trigonometry] [Complex Variables]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus