APPLICATIONS OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS

(Amortization Word Problems)

To solve an exponential or logarithmic word problem, convert the narrative to an equation and solve the equation.
There is a relationship between the mortgage amount, the number of payments, the amount of the payment, how often the payment is made, and the interest rate. The following formulas illustrate the relationship:

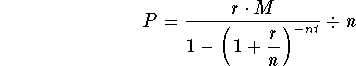
where P = the payment, r = the annual rate, M = the mortgage amount, t = the number of years, and n = the number of payments per year.

Problem 4: Suppose you need to take out a mortgage of $100,000. All you can afford for monthly payments is $800. You will retire in 25 years; therefore, the longest you can make these payments is 25 years. What interest rate would you need to take out a mortgage of $100,000 and pay it back in 300 monthly payments of $800

Answer: 8.42%

Solution and Explanations:

Step 1: In the equation

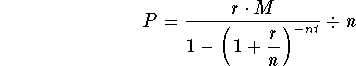
substitute $100,000 for M (the mortgage amount), 12 for n (the number of payments per year, $800 for P (the monthly payment), and 25 for t (the term of the mortgage in years). You are solving for r (the annual interest rate)

Step 2: We are going to solve this problem by iteration (trial and error). Let's start with an interest rate of 9%. Substitute .09 for r in the right side of the above equation and compare it to the $800 on the left side of the equation.
If, after the substitution, the value of the right side is lower than $800, it means that your guess of 9% was too low. If, after the substitution, the value of the right side is higher than $800, it means that your guess of 9% was too high.

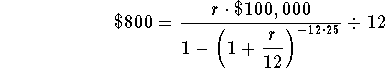
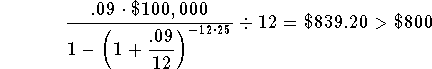
The value of the right side of the equation, using r = 9%, is higher than $800. This means that your guess of 9% for the rate was too high.

Step 3: Try 8%:

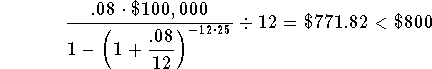
The value of the right side of the equation, using r = 8%, is lower than $800. This means that your guess of 8% for the rate was too low. Since 9% was too high and 8% was too low, the real rate is between 8% and 9%.

Step 4: Try 8.5%:

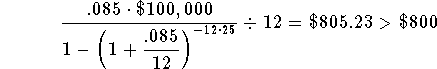
The value of the right side of the equation, using r = 8.5%, is a littler higher than $800. This means that your guess of 8.5% for the rate was a little high. Since 8.5% was too high and 8% was too low, the real rate is between 8% and 8.5%. Since $805.23 is very close to $800, the real rate is close to 8.5%.

Step 5: Try 8.4%:

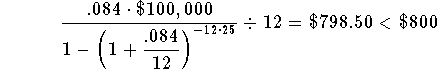
The value of the right side of the equation, using r = 8.4%, is a little lower than $800. This means that your guess of 8.4% for the rate was too low. Since 8.5% was too high and 8.4% was too low, the real rate is between 8.4% and 8.5%.

Step 6: Try 8.45%:

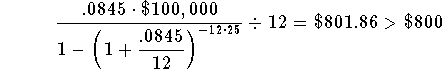
The value of the right side of the equation, using r = 8.45%, is a little higher than $800. This means that your guess of 8.45% for the rate was a little high. Since 8.45 was too high and 8.4% was too low, the real rate is between 8.4% and 8.45%.

Step 7: Try 8.42%:

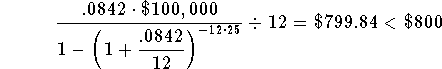
The value of the right side of the equation, using r = 8.42%, is lower than $800. This means that your guess of 8.42% for the rate was close but still too low. Since 8.45% was too high and 8.42% was too low, the real rate is between 8.42% and 8.45%.

Step 8: Try 8.43%:

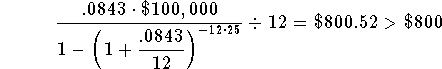
The value of the right side of the equation, using r = 8.43%, is very close but still higher than $800. This means that your guess of 8.43% for the rate was too low. Since 8.42% was too high and 8.43% was too low, the real rate is between 8.42% and 8.43%.

Step 9: Try 8.422%:

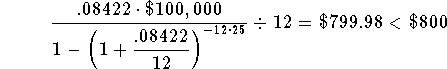
The value of the right side of the equation, using r = 8.422%, is very close but still lower than $800. This means that your guess of 8.422 % for the rate is very close but still a little . Since 8.43% was too high and 8.422% was too low, the real rate is between 8.422% and 8.43%.

Step 10: Try 8.423%:

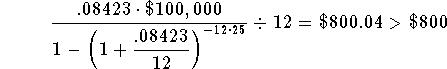
The value of the right side of the equation, using r = 8.423%, is higher than $800. This means that your guess of 8.423% for the rate was too high. Since 8.423% was too high and 8.422% was too low, the real rate is between 8.422% and 8.423%.

We could keep on until you reached the degree of accuracy you desired. However, most banks round to four decimals. Since both 8.422% and 8.423% rounded to 8.42%, that is our answer.

If you would like to review the log menu click on log menu.

If you would like to review the general menu, click on menu below.

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.