APPLICATIONS OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS

APPLICATIONS OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS

(Population Word Problems)

To solve an exponential or logarithmic word problem, convert the narrative to an equation and solve the equation.

In this section, we will review population problems.

Example 4: Suppose that you are observing the behavior of cell duplication in a lab. In one experiment, you start with one cell and the cell population is tripling every minute. Write an equation with base 3 to determine the number of cells after one hour.

Solution and Explanations:

First record your observations by making a table with two columns: one column for the time and one column for the number of cells. The number of cells (population size) depends on the time. If you were to graph your findings, the points would be formed by (specific time, number of cells at the specific time). For example at t = 0, there is 1 cell, and the corresponding point is (0, 1). At t = 1, there are 3 cells, and the corresponding point is (1, 3). At t = 2, there are 9 cells, and the corresponding point is (2, 9). At t = 3, there are 27 cells, and the corresponding point is (3, 27).

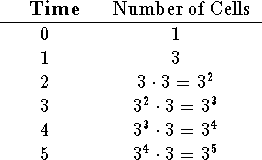
You can see that the relationship between the two parts of the point is exponential where the exponent is the time. Therefore, we say that the equation that reflects the (number) size of the population at time t is

Let's check it by estimating the population after 10 minutes with the formula and with the table. By the formula,

By the table, after 10 minutes the population is

Therefore the formula is

Determine the number of cells after one hour:

Solution and Explanation:

• Convert one hour to minutes. .

• Substitute 60 for t in the equation :

  

Example 5: Determine how long it would take the number of cells (population) to reach 100,000 cells.

Solution and explanation:

• Here you know the number of cells at the beginning of the study (1) and the number of cells at the end of the study (100,000), but you do not know the time. Substitute 100,000 for f(t) in the equation :

  

• Take the natural logarithm of both sides:

  

• Simplify the right side of the equation using the third rule of logarithms:

  

• Divide both sides by and simplify:

  

It would take a little more than 10 minutes for the number (population) of cells to reach 100,000.

Example 6: Write an equation with base 10 that is equivalent to the equation .

Solution and Explanation:

• Let's start with a generic exponential equation with base 10:

  

• The f(t) represents the size of the population at time t, and t represents the time. The the a and b represent adjusters when we change the base. You will see that a always represents the size of the population at the start of the study and b is the relative growth rate. The value of b will vary depending upon what base you use in your equation. Therefore, you need to find the value of a and b for base 10.

• You know that the population is 1 at time 0, so insert these numbers in the equation . You now have

  

  You now know that the value of a in the adjusted equation is 1. You really already knew this since the number of cells at time 0 was 1.

• Rewrite the equation with a = 1.

  

  which in turn can be rewritten as

  

• From observation, we know that the population after 1 minute was 3 cells, so insert these numbers in the equation ; let t = 1 and f(t) = 3:

  

• Solve for b by taking the natural logarithm of both sides of the equation

  

• Simplify the right side of the equation using the third rule of logarithms:

  

• Divide both sides of the equation by and simplify:

  

  rounded to 0.4771.

• Insert this value of b in the equation

  and the equation is simplified to

  

• We know that the population is 27 after 3 minutes, so use these values to check the validity of the above equation. Substitute 3 for t in the right side of the above equation. If the answer is 27, or close to 27 because we rounded, then the model is correct.

  

  rounded to 27. Remember the check won't be exact because we rounded 0.47712154721 to 0.477.

• We know from the original equation that after 4 seconds, the population is 81. Let's do a second check. , rounded to 81 cells. We could have gotten even closer by taking b out to more decimals.

The equation

with base 10 is equivalent to the equation

with base 3.

By now you may have concluded that in the equation , the value of a is the size of the population at time zero and b is the relative growth rate with respect to the base e. If b is positive, the population is growing. If b is negative, the population is declining.

If you would like to work another example, click on Example

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.