 APPLICATIONS OF EXPONENTIAL AND
APPLICATIONS OF EXPONENTIAL AND  APPLICATIONS OF EXPONENTIAL AND
APPLICATIONS OF EXPONENTIAL AND 
(Population Word Problems)
To solve an exponential or logarithmic word problem, convert the narrative to an equation and solve the equation. In this section, we will review population problems.
Problem 6: Town A had a population of 10,000 in 1900 and 20,000
in 1950. Town B had a population 60,000 in 1900 and 15,000 in
1950. In what year was the population in both towns the same?
Solution and Explanations:
In this problem, we will first have to find an exponential equation
for each town. You could use any exponential equation of the
form
Town A:
The points on the graph of the function f(t) will be (specific time, and population at that time). Let's let t = 0 at the start of our study or 1900. Therefore, our first point is (0, 10,000). The second point corresponds to the year 1950 where t = 50 (1950 - 1900). The second point is (50, 20,000).
rounded to 0.0139.
The f(t) stands for the population t years after the start of the study, the 10,000 is the population at the start of the study, the 0.0139 is the relative growth rate, and t equals the number of years since the start of the study
in 1900.
The equation that best fits the population trend of Town A is
Town B:
The points on the graph of the function f(t) will be (specific time, and population at that time). Let's let t = 0 at the start of our study or 1900. Therefore, our first point is (0, 60,000). The second point corresponds to the year 1950 where t = 50 (1950 - 1900). The second point is (50, 15,000).
We will use these two points to find the value of c and the value
of d in the equation
rounded to -0.0277.
The g(t) stands for the population t years after the start of the study, the 60,000 is the population at the start of the study, the -0.0277 is the relative growth rate, and t equals the number of years since the start of the study in 1900.
The equation that best fits the population trend of Town B
We are trying to determine in what year the population size was
the same for these two town.. Since f(t) represents the size
of the population of Town A and g(t) represents the size of the
population of Town B, set f(t) equal to g(t) and solve for t.
When t = 43, or in the year 1943 (1900 + 43), the population
of Town A and the population of Town B would be the same size. Let's check this number.
Town A: Insert t = 43 in the equation
Town B: Insert t = 43 in the equation
Close enough check. Remember the check will not be exact because
we rounded the relative growth rates. Therefore, in 1943, the
population of Town A and the population of Town B will be between 18,179 and 18,233.
If you would like to revisit other topics click on menu below.
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.
![]() , where B is any positive number greater than
0, to solve this problem. For standardization sake, let's use
the base e. Let the equation
, where B is any positive number greater than
0, to solve this problem. For standardization sake, let's use
the base e. Let the equation ![]() represent the population pattern for Town A, and let the equation
represent the population pattern for Town A, and let the equation ![]() represent the population pattern for Town B.
represent the population pattern for Town B.
We will use these two points to find the value of a and the value
of b in the equation
![]()
![]() :
:
![]()
![]() and we have
and we have
![]()
![]() and we have
and we have
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() and we have
and we have
![]()
![]() and we have
and we have
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
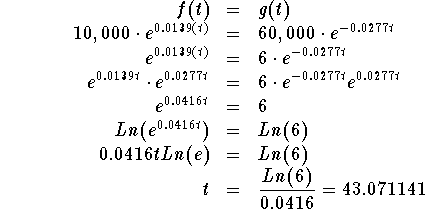
![]()
![]()
![]()
![]()

 S.O.S MATHematics home
page
S.O.S MATHematics home
page 
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour