APPLICATIONS OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS

	APPLICATIONS OF EXPONENTIAL
	AND
	LOGARITHMIC FUNCTIONS

DECAY WORD PROBLEMS:

To solve an exponential or logarithmic word problem, convert the narrative to an equation and solve the equation.

Example 4: Alpino, New Mexico had a population of 20,000 in 1900 and a population of 5,000 in 1995. The population decline followed an exponential model. What was the population in 1950? If we can assume that the model holds into the future, in what year will the city have less than 10 people? Use the base 10 to find your answers.

Solution and Explanation:

Let's us form the equation with base 10:

$\begin{eqnarray*}f\left( t\right) &=&a\cdot 10^{bt} \end{eqnarray*}$

Let's call 1900 time 0. The population in 1900 was 20,000.

$\begin{eqnarray*}f\left( 0\right) &=&20,000. \end{eqnarray*}$

The equation is now

$\begin{eqnarray*}f\left( t\right) &=&20,000\cdot 10^{bt}. \end{eqnarray*}$

In 1995 when t=95, the population was 5,000. Another way of saying this is

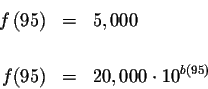
$\begin{eqnarray*}f\left( 95\right) &=&5,000 \\ && \\ f(95) &=&20,000\cdot 10^{b\left( 95\right) } \end{eqnarray*}$

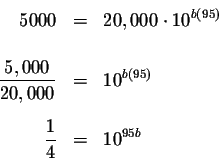
$\begin{eqnarray*}5000 &=&20,000\cdot 10^{b\left( 95\right) } \\ && \\ \display... ...ft( 95\right) } \\ && \\ \displaystyle \frac{1}{4} &=&10^{95b} \end{eqnarray*}$

Take the common log of both sides of the equation.

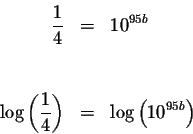
$\begin{eqnarray*}\displaystyle \frac{1}{4} &=&10^{95b} \\ && \\ && \\ \log \l... ... \displaystyle \frac{1}{4}\right) &=&\log \left( 10^{95b}\right) \end{eqnarray*}$

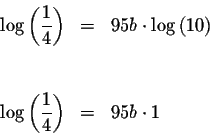
$\begin{eqnarray*}\log \left( \displaystyle \frac{1}{4}\right) &=&95b\cdot \log \... ...& \\ \log \left( \displaystyle \frac{1}{4}\right) &=&95b\cdot 1 \end{eqnarray*}$

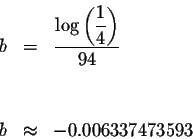
$\begin{eqnarray*}b &=&\displaystyle \frac{\log \left( \displaystyle \frac{1}{4}\right) }{94} \\ && \\ && \\ b &\approx &-0.006337473593 \end{eqnarray*}$

The equation can be written as

$\begin{eqnarray*}f\left( t\right) &=&20,000\cdot 10^{-0.006337473593t} \end{eqnarray*}$

In 1950, t=50. Just substitute 50 for t in the equation.

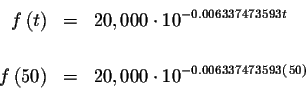
$\begin{eqnarray*}f\left( t\right) &=&20,000\cdot 10^{-0.006337473593t} \\ && \\... ...( 50\right) &=&20,000\cdot 10^{-0.006337473593\left( 50\right) } \end{eqnarray*}$

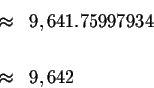
$\begin{eqnarray*}&\approx &9,641.75997934 \\ && \\ &\approx &9,642 \end{eqnarray*}$

In the year 1950 the population was 9,642.

In what year will the population be less than 10 people? Substitute 10 for $f\left( t\right) .$

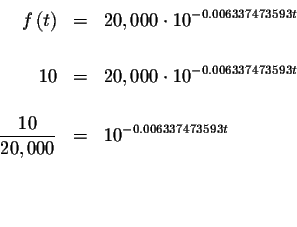
$\begin{eqnarray*}f\left( t\right) &=&20,000\cdot 10^{-0.006337473593t} \\ && \\... ... \frac{10}{20,000} &=&10^{-0.006337473593t} \\ && \\ && \\ && \end{eqnarray*}$

Take the common log of both sides of the equation.

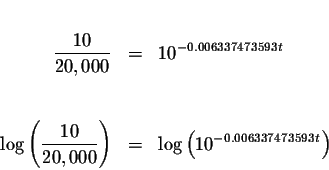
$\begin{eqnarray*}&& \\ \displaystyle \frac{10}{20,000} &=&10^{-0.006337473593t}... ...c{10}{20,000}\right) &=&\log \left( 10^{-0.006337473593t}\right) \end{eqnarray*}$

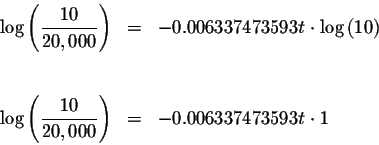
$\begin{eqnarray*}\log \left( \displaystyle \frac{10}{20,000}\right) &=&-0.006337... ...displaystyle \frac{10}{20,000}\right) &=&-0.006337473593t\cdot 1 \end{eqnarray*}$

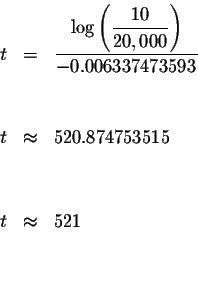
$\begin{eqnarray*}t &=&\displaystyle \frac{\log \left( \displaystyle \frac{10}{20... ...x &520.874753515 \\ && \\ && \\ t &\approx &521 \\ && \\ && \end{eqnarray*}$

In the year 1900 + 521 or in the year 2421, the population will be less than 10.

If you would like to test your knowledge by working some problems, click on problem.

If you would like to go back to the table of contents, click on contents.

[Exponential Rules] [Logarithms]

[Algebra] [Trigonometry ] [Complex Variables]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus