APPLICATIONS OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS

	APPLICATIONS OF EXPONENTIAL
	AND
	LOGARITHMIC FUNCTIONS

DECAY WORD PROBLEMS:

Problem 2: If a radioactive substance has a half-life of 300 years, how long will it take for the substance to decay to 10 percent of its initial amount?

Answer: 997 years

Solution:

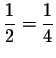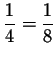What does it mean to say that a substance has a half-life of 300 years? It means that every 300 years half of the substances disappears. After the first 300 years, one-half remains, after the second 300 years only one $\displaystyle \frac{1}{2}$ of $\displaystyle \frac{1}{2}=\displaystyle \frac{1}{4}$ remains, after the third 300 years, only $\displaystyle \frac{1}{2}$ of $\displaystyle \frac{1}{4}=\displaystyle \frac{1}{8}$ remains and so forth.

Let's create some points that describe the experiment and plot these points. Examine the graph to determine what type of function we are dealing with. All the points will have the form ( number of years, percent of substance remaining)

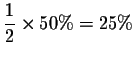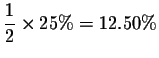At time 0, 100% of the substance is present; the corresponding point is $\left( 0,1\right) .$ After 300 years only 50% of the substance is present; the corresponding point is $\left( 300,0.50\right) .$ After 600 years only $\displaystyle \frac{1}{2}\times 50\%=25\%$ of the substance is present; the corresponding point is $\left( 600,0.25\right) .$ After 900 years only $\displaystyle \frac{1}{2}\times 25\%=12.50\%$ of the substance is present. 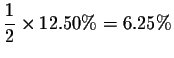After 1200 years only $\displaystyle \frac{1}{2 }\times 12.50\%=6.25\%$ of the substance is present; the corresponding point is $\left( 1200,0.625\right)$ .

When you plot the data, the curve looks exponential. Therefore, the mathematical model is probably exponential The model looks something like

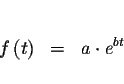
$\begin{eqnarray*}&& \\ f\left( t\right) &=&a\cdot e^{bt} \\ && \end{eqnarray*}$

where $f\left( t\right)$ represents the percent of the initial substance remaining after t years, a represents the initial percent of the substance (either 100% or 1.00), t represents the numbers of years that have passed, and b represents the decay constant based on a base of e.(Note that you can use any base. The base e is chosen for standardization purposes only).

We know that $a=100\%$ or 1.00. However, you can verify it in the equation $f\left( t\right) =a\cdot e^{bt}.$ Let t=0 in the equation.

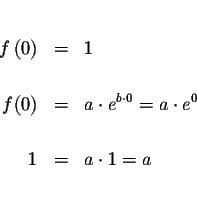
$\begin{eqnarray*}&& \\ f\left( 0\right) &=&1 \\ && \\ f(0) &=&a\cdot e^{b\cdot 0}=a\cdot e^{0} \\ && \\ 1 &=&a\cdot 1=a \\ && \\ && \end{eqnarray*}$

The equation is now modified:

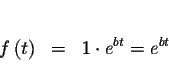
$\begin{eqnarray*}&& \\ f\left( t\right) &=&1\cdot e^{bt}=e^{bt} \\ && \end{eqnarray*}$

We know that $50\%$ or 0.50 of the initial substance remains after 300 years. Another way of saying this is that $f\left( 300\right) =0.50.$ In the above equation, replace $f\left( 300\right)$ with 0.50 and replace twith 300.

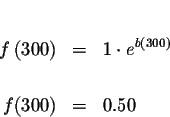
$\begin{eqnarray*}&& \\ f\left( 300\right) &=&1\cdot e^{b\left( 300\right) } \\ && \\ f(300) &=&0.50 \end{eqnarray*}$

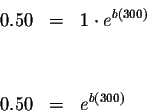
$\begin{eqnarray*}0.50 &=&1\cdot e^{b\left( 300\right) } \\ && \\ && \\ 0.50 &=&e^{b\left( 300\right) } \end{eqnarray*}$

Take the natural logarithm of both sides of the equation:

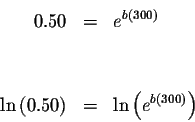
$\begin{eqnarray*}0.50 &=&e^{b\left( 300\right) } \\ && \\ && \\ \ln \left( 0.50\right) &=&\ln \left( e^{b\left( 300\right) }\right) \end{eqnarray*}$

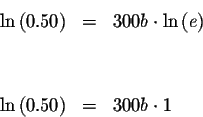
$\begin{eqnarray*}\ln \left( 0.50\right) &=&300b\cdot \ln \left( e\right) \\ && \\ && \\ \ln \left( 0.50\right) &=&300b\cdot 1 \end{eqnarray*}$

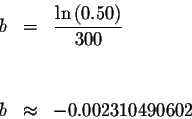
$\begin{eqnarray*}b &=&\displaystyle \frac{\ln \left( 0.50\right) }{300} \\ && \\ && \\ b &\approx &-0.002310490602 \end{eqnarray*}$

The equation describing the percentage of initial remaining after a certain number of years is

$\begin{eqnarray*}f\left( t\right) &=&1\cdot e^{-0.002310490602\cdot t} \end{eqnarray*}$

Let's check it out by seeing if this model will give us 0.25 after 600 years.

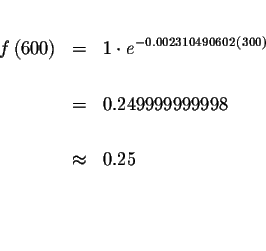
$\begin{eqnarray*}&& \\ f\left( 600\right) &=&1\cdot e^{-0.002310490602\left( 30... ...&=&0.249999999998 \\ && \\ &\approx &0.25 \\ && \\ && \\ && \end{eqnarray*}$

The model is $f\left( t\right) =1\cdot e^{-0.002310490602\left( t\right) }$ or $f\left( t\right) =e^{-0.002310490602\left( t\right) }$

How long will it take the sample to decay to 10% of its initial amount?? Just substitute 0.10 for $f\left( t\right)$ in the equation.

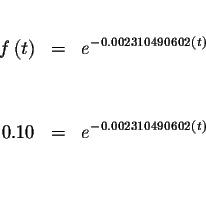
$\begin{eqnarray*}&& \\ f\left( t\right) &=&e^{-0.002310490602\left( t\right) } ... ...0.10 &=&e^{-0.002310490602\left( t\right) } \\ && \\ && \\ && \end{eqnarray*}$

Take the natural logarithm of both sides of the equation.

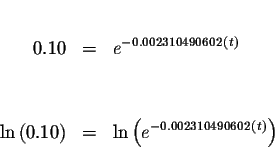
$\begin{eqnarray*}&& \\ 0.10 &=&e^{-0.002310490602\left( t\right) } \\ && \\ &... ...\right) &=&\ln \left( e^{-0.002310490602\left( t\right) }\right) \end{eqnarray*}$

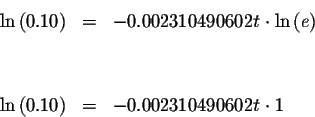
$\begin{eqnarray*}\ln \left( 0.10\right) &=&-0.002310490602t\cdot \ln \left( e\ri... ... && \\ && \\ \ln \left( 0.10\right) &=&-0.002310490602t\cdot 1 \end{eqnarray*}$

$\begin{eqnarray*}t &=&\displaystyle \frac{\ln \left( 0.10\right) }{-0.002310490602} \\ && \\ && \\ t &\approx &996.578428409122.877013985 \end{eqnarray*}$

It will take about 997 years (rounded) for 90% of the initial substance to decay leaving just 10%.

If you would like to review problem 3, click on Problem 3

If you would like to go back to the table of contents, click on contents.

[Exponential Rules] [Logarithms]

[Algebra] [Trigonometry ] [Complex Variables]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus