APPLICATIONS OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS

	APPLICATIONS OF EXPONENTIAL
	AND
	LOGARITHMIC FUNCTIONS

EARTHQUAKE WORD PROBLEMS:

As with any word problem, the trick is convert a narrative statement or question to a mathematical statement.

Before we start, let's talk about earthquakes and how we measure their intensity.

In 1935 Charles Richter defined the magnitude of an earthquake to be

$\begin{eqnarray*}M &=&\log \displaystyle \frac{I}{S} \end{eqnarray*}$

where I is the intensity of the earthquake (measured by the amplitude of a seismograph reading taken 100 km from the epicenter of the earthquake) and S is the intensity of a ''standard earthquake'' (whose amplitude is 1 micron =10^-4 cm).

The magnitude of a standard earthquake is

$\begin{eqnarray*}M &=&\log \displaystyle \frac{S}{S}=\log 1=0 \end{eqnarray*}$

Richter studied many earthquakes that occurred between 1900 and 1950. The largest had magnitude of 8.9 on the Richter scale, and the smallest had magnitude 0. This corresponds to a ratio of intensities of 800,000,000, so the Richter scale provides more manageable numbers to work with.

Each number increase on the Richter scale indicates an intensity ten times stronger. For example, an earthquake of magnitude 6 is ten times stronger than an earthquake of magnitude 5. An earthquake of magnitude 7 is $10\times 10=100$ times strong than an earthquake of magnitude 5. An earthquake of magnitude 8 is $10\times 10\times 10=1000$ times stronger than an earthquake of magnitude 5.

Example 5: The 1985 Mexico City earthquake had a magnitude of 8.1 on the Richter scale and the 1976 Tangshan earthquake was 1.26 as intense. What was the magnitude of the Tangshan earthquake?

Solution: Convert the sentence ''The 1985 Mexico City earthquake had a magnitude of 8.1 on the Richter scale.'' to an equivalent mathematical equation.

$\begin{eqnarray*}8.1 &=&\log \displaystyle \frac{I_{Mexico}}{S} \end{eqnarray*}$

Convert the ''The 1976 Tangshan earthquake was 1.26 as intense.'' to an equivalent mathematical equation.

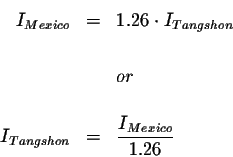
$\begin{eqnarray*}I_{Mexico} &=&1.26\cdot I_{Tangshon} \\ && \\ &&or \\ && \\ I_{Tangshon} &=&\displaystyle \frac{I_{Mexico}}{1.26} \end{eqnarray*}$

where I_Mexico is the intensity of the Mexico City earthquake and I_Tangshon is the intensity of the Tangshon earthquake.

We are trying to determine the magnitude of the Tangshon earthquake.

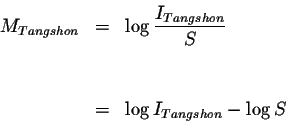
$\begin{eqnarray*}M_{Tangshon} &=&\log \displaystyle \frac{I_{Tangshon}}{S} \\ && \\ && \\ &=&\log I_{Tangshon}-\log S \end{eqnarray*}$

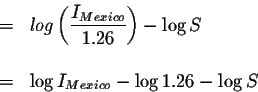
$\begin{eqnarray*}&=&log\left( \displaystyle \frac{I_{Mexico}}{1.26}\right) -\log S \\ && \\ &=&\log I_{Mexico}-\log 1.26-\log S \end{eqnarray*}$

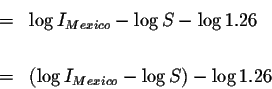
$\begin{eqnarray*}&=&\log I_{Mexico}-\log S-\log 1.26 \\ && \\ &=&\left( \log I_{Mexico}-\log S\right) -\log 1.26 \end{eqnarray*}$

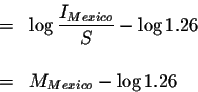
$\begin{eqnarray*}&=&\log \displaystyle \frac{I_{Mexico}}{S}-\log 1.26 \\ && \\ &=&M_{Mexico}-\log 1.26 \end{eqnarray*}$

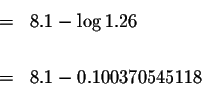
$\begin{eqnarray*}&=&8.1-\log 1.26 \\ && \\ &=&8.1-0.100370545118 \end{eqnarray*}$

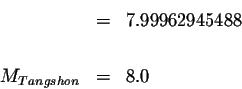
$\begin{eqnarray*}&=&7.99962945488 \\ && \\ M_{Tangshon} &=&8.0 \end{eqnarray*}$

Let's check our answer:

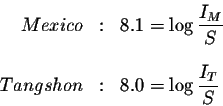
$\begin{eqnarray*}Mexico &:&8.1=\log \displaystyle \frac{I_{M}}{S} \\ && \\ Tangshon &:&8.0=\log \displaystyle \frac{I_{T}}{S} \end{eqnarray*}$

Convert both of these equations to exponential equations.

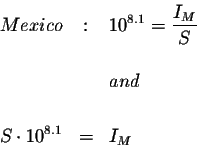
$\begin{eqnarray*}Mexico &:&10^{8.1}=\displaystyle \frac{I_{M}}{S} \\ && \\ &&and \\ && \\ S\cdot 10^{8.1} &=&I_{M} \end{eqnarray*}$

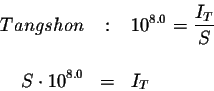
$\begin{eqnarray*}Tangshon &:&10^{8.0}=\displaystyle \frac{I_{T}}{S} \\ && \\ S\cdot 10^{8.0} &=&I_{T} \end{eqnarray*}$

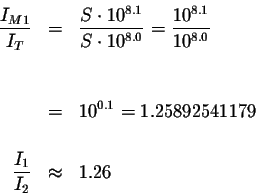
$\begin{eqnarray*}\displaystyle \frac{I_{M1}}{I_{T}} &=&\displaystyle \frac{S\cdo... ...1179 \\ && \\ \displaystyle \frac{I_{1}}{I_{2}} &\approx &1.26 \end{eqnarray*}$

Example 6: If the intensity of earthquake A is 5 and the intensity of earthquake B is 650, what is the difference in their magnitudes as measured by the Richter scale?

Solution: The magnitudes $\left( M\right)$ of each earthquake is different. Let M_L represent the intensity the earthquake with the greater intensity and M_S represent the earthquake with the smaller intensity.

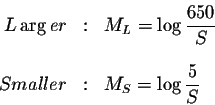
$\begin{eqnarray*}L\arg er &:&M_{L}=\log \displaystyle \frac{650}{S} \\ && \\ Smaller &:&M_{S}=\log \displaystyle \frac{5}{S} \end{eqnarray*}$

What you are looking for is the ratio of the intensities: M_L-M_S. So our task is to isolate this expression from the above given information using the rules of logarithms.

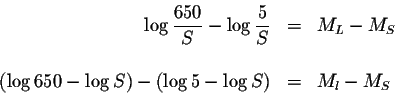
$\begin{eqnarray*}\log \displaystyle \frac{650}{S}-\log \displaystyle \frac{5}{S}... ...og 650-\log S\right) -\left( \log 5-\log S\right) &=&M_{l}-M_{S} \end{eqnarray*}$

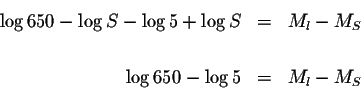
$\begin{eqnarray*}\log 650-\log S-\log 5+\log S &=&M_{l}-M_{S} \\ && \\ \log 650-\log 5 &=&M_{l}-M_{S} \end{eqnarray*}$

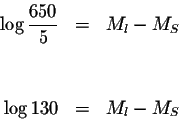
$\begin{eqnarray*}\log \displaystyle \frac{650}{5} &=&M_{l}-M_{S} \\ && \\ && \\ \log 130 &=&M_{l}-M_{S} \end{eqnarray*}$

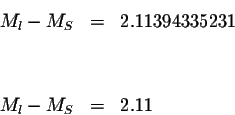
$\begin{eqnarray*}M_{l}-M_{S} &=&2.11394335231 \\ && \\ && \\ M_{l}-M_{S} &=&2.11 \end{eqnarray*}$

The difference between the magnitudes of the two earthquakes is 2.11 on the Richter scale.

Let's check the answer.

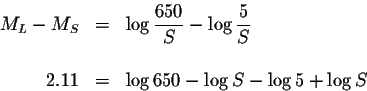
$\begin{eqnarray*}M_{L}-M_{S} &=&\log \displaystyle \frac{650}{S}-\log \displaystyle \frac{5}{S} \\ && \\ 2.11 &=&\log 650-\log S-\log 5+\log S \end{eqnarray*}$

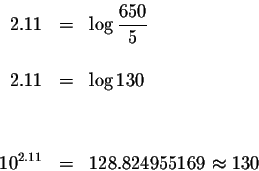
$\begin{eqnarray*}2.11 &=&\log \displaystyle \frac{650}{5} \\ && \\ 2.11 &=&\log 130 \\ && \\ && \\ 10^{2.11} &=&128.824955169\approx 130 \end{eqnarray*}$

It will not check exactly because we rounded the 2.11, but it is sufficiently close to check our answer.

If you would like to test your knowledge by working some problems, click on problem.

If you would like to go back to the table of contents, click on contents.

[Exponential Rules] [Logarithms]

[Algebra] [Trigonometry ] [Complex Variables]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus