EQUATIONS CONTAINING VARIABLES UNDER ONE OR MORE RADICALS

Note:

• In order to solve for x, you must isolate x.

• In order to isolate x, you must remove it from under the radical.

• If there is just one radical in the equation, isolate the radical.

• Then raise both sides of the equation to a power equal to the index

  of the radical.

• With these types of equations, sometimes there are extraneous

  solutions; therefore, you must check your answers.

• If the index of the radical is even, many times there will be a

  restriction on the values of x.

Problem 2.1b:

First make a note of the fact that you cannot take the square root of a negative number.

Therefore,

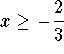
Square both sides of the equation.

Subtract 2 from both sides of the equation

Divide both sides of the equation by 3.

The answer is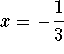

Check the solution by substituting in the original equation

for x. If the left side of the equation equals the right side of the

equation after the substitution, you have found the correct answer.

If you would like to review the solution for Problem 2.1c, click on Solution.

If you would like to go to the problem page again, click on problem.

If you would like to go back to the equation table of contents, click on contents.

[Algebra] [Trigonometry] [Geometry] [Differential Equations] [Calculus] [Complex Variables]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.


Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour