EQUATIONS CONTAINING VARIABLES UNDER ONE OR MORE RADICALS

Note:

• In order to solve for x, you must isolate x.
• In order to isolate x, you must remove it from under the radial.
• If there are two radicals in the equation,isolate one of the radicals.
• Then raise both sides of the equation to a power equal to the index of the isolated radical.
• Isolate the remaining radical.
• Raise both sides of the equation to a power equal to the index of the isolated radical.
• You should now have a polynomial equation. Solve it.
• Remember that you did not start out with a polynomial; therefore, there may be extraneous solutions. Therefore, you must check your answers.

Example 3:

First make a note of the fact that you cannot take the square root of a negative number. Therefore,the first term is valid only if 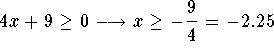and the second term is valid if 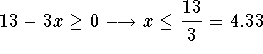. Therefore, the domain is restricted to the set of real numbers x, .

Isolate the term

Square both sides of the equation.

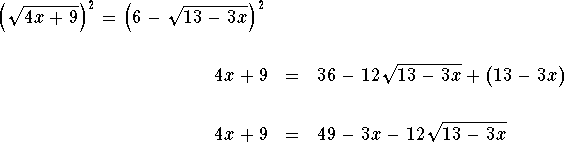
Isolate the term.

Square both sides of the equation.

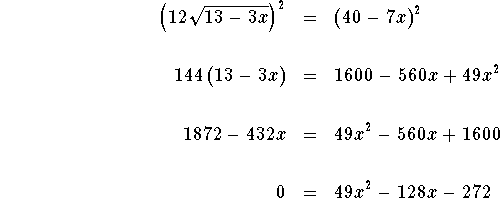
Solve for x using the quadratic formula.

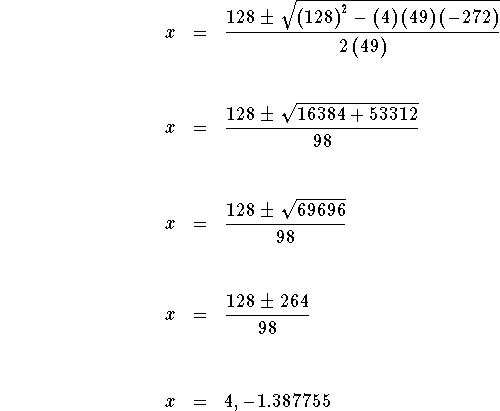
There is one exact answer of 4 and one approximate answer of -1.387755.

Check the solution 4 by substituting 4 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

• Left side:

• Right Side: 6

Since the left side of the original equation equals the right side of the original equation after we substituted our solution for x, we have verified that the solutions is x=4.

Check the solution -1.387755 by substituting -1.387755 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

• Left side:

• Right Side:6

Since the left side of the original equation equals the right side of the original equation after we substituted our solution for x, we have verified that the solutions is x=-1.387755.

You can also check the answer by graphing the equation:

The graph represents the right side of the original equation minus the left side of the original equation. The x-intercept(s) of this graph is(are) the solution(s). Since the x-intercepts are 4 and -1.387755, we have verified the solutions.

If you would like to review another example, click on Example

If you would like to test yourself by working some problems similar to this example, click on Problem.

If you would like to go back to the equation table of contents, click on Contents.

[Algebra] [Trigonometry] [Geometry] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour