SOLVING EQUATIONS CONTAINING ABSOLUTE VALUE(S)

Note:

• if and only if

• if and only if a+b=3 or a+b=-3

• Step 1:Isolate the absolute value expression.

• Step 2:Set the quantity inside the absolute value notation equal to + and - the quantity on the other side of the equation.

• Step 3:Solve for the unknown in both equations.

• Step 4:Check your answer analytically or graphically.

Solve for x in the following equation.

Problem 3.1a:

Step 2:Set the quantity within the absolute value notation to

Step 3:Solve for x in the equation 4x-7=3:

Step 4:Solve for x in the equation 4x-7=-3:

The answers are and x=1. However these answers may not be the solutions to the original equation. You must check your answers.

Step 5:Check the solutions.

Check the solution by substituting in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

• Left Side:

• Right Side:

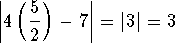
Since the left side of the original equation after we substituted the value for, the solution is valid

Check the solution x = 1 by substituting 1 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

• Left Side:

• Right Side:

  
  

  
  

Since the left side of the original equation after we substituted the value 1 for, the solution x=1 is valid

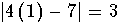
You can also check your answer by graphing (the left side of the original equation minus the right side of the original equation). You will note that the two x-intercepts on the graph are located at 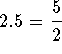and 1

If you would like to review the solution to problem 3.1b, click on Solution

If you would like to go back to the problem page, click on Problem

If you would like to go back to the equation table of contents, click on Contents.

[Algebra] [Trigonometry] [Geometry] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour