SOLVING EQUATION CONTAINING ABSOLUTE VALUE(S)

Note:

if and only if
if and only if a + b = 3 or a + b = -3
if any only if a + b = +(x + y) or a + b = -(x + y)

Solve for x in the following equation.

Example 5:

Either or

Solve

eqnarray29

eqnarray34

Solve

eqnarray51

eqnarray56

The answers are 1.70156211872, -4.70156211872, 1.27491721764 and -6.27491721764. These answers may or may not be solutions to the original equation. You must verify each of the answers.

Check the solutions:

Check the answer x=1.70156211872 by substituting 1.70156211872 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

Left Side:
Right Side:

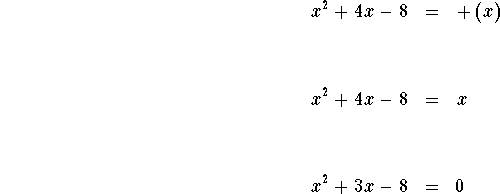
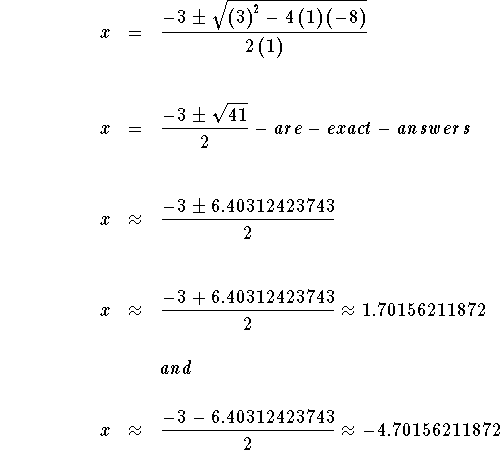
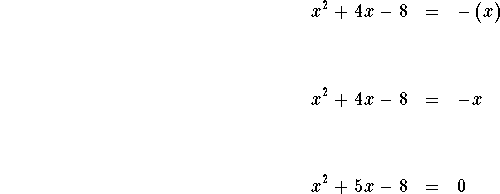
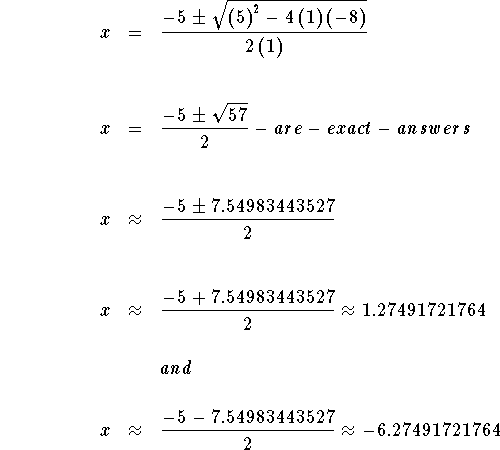
Since the left side of the original equation is equal to the right side of the original equation after 1.70156211872 was substituted for x, the answer x=1.70156211872 is a solution to the original equation.

Check x=-4.70156211872 by substituting -4.70156211872 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

Left Side:
Right Side:

Since the left side of the original equation is not equal to the right side of the original equation after -4.70156211872 is substituted for x, the answer x=-4.70156211872 is a not solution to the original equation.

Check x=1.27491721764 by substituting 1.27491721764 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

Left Side:
Right Side:

Since the left side of the original equation is equal to the right side of the original equation after 1.27491721764 was substituted for x, the answer x=1.27491721764 is a solution to the original equation.

Check x=-6.27491721764 by substituting -6.27491721764 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

Left Side:
Right Side:

Since the left side of the original equation is not equal to the right side of the original equation after -6.27491721764 was substituted for x, the answer x=-6.27491721764 is not a solution to the original equation. Since we rounded the solution, the check will not be exact.

The solutions are x=1.70156211872 and 1.27491721764.

You can also check your answer by graphing

The graph was formed by subtracting the right side of the original equation from the left side of the original equation. You will note that there are two x-intercepts on the graph are located at x=1.70156211872 and 1.27491721764. This verifies the two solutions by a graphical method.

If you would like to work another example, click on example.

If you would like to test yourself by working some problems similar to this example, click on problem.

If you would like to go back to the equation table of contents, click on contents.

[Algebra] [Trigonometry] [Geometry] [Differential Equations] [Calculus] [Complex Variables] [Matrix]

S.O.S. MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus