Note:
If you would like an in-depth review of fractions, click on Fractions.
Solve for x in the following equation.
Problem 5.2a:
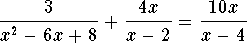
Answer :
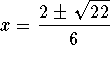are the exact answers
and 
are the approximate answers.
Comment on answers: You may wonder why we give you the answers in two forms: exact and approximate. There is a reason. Students seem perplexed when they think they have worked a problem correctly and yet, their exact answers differ from the exact answers in the book. The student is not necessarily wrong. Depending on the method chosen to work the problem, exact answers have a different look. How do you know whether your exact answer is equivalent to a different looking exact answer in the book? Simplify both. If both exact answers are correct, they will both simplify to the same approximate answer.
Next time your answer differs from the answer in the book, simplify both. If
the approximate answers are the same, you are correct. If not, go back to
the drawing board and try to find your mistake.
Solution:
Rewrite the problem so that every denominator is factored
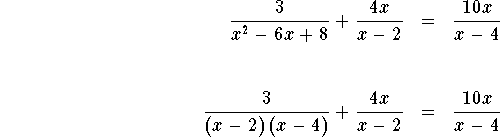
Recall that you cannot divide by zero. Therefore, the first fraction is
valid if , 
or 
the second fraction is
valid if 
and the third fraction is valid is 
.If either 
or 
turn out to be
the solutions, you must discard them as extraneous solutions.
Multiply both sides by the least common multiple 
(the smallest number that all the denominators
will divide into evenly). This step will eliminate all the
denominators.
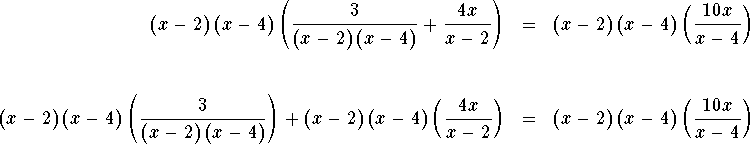
which is equivalent to
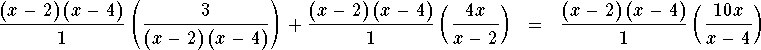
which can be rewritten as
which can be rewritten as
which can be simplified to
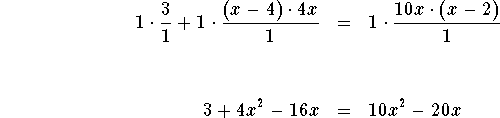
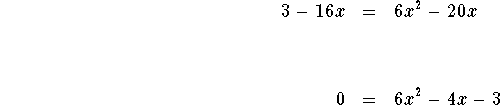
Solve for x using the quadratic formula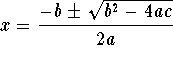 
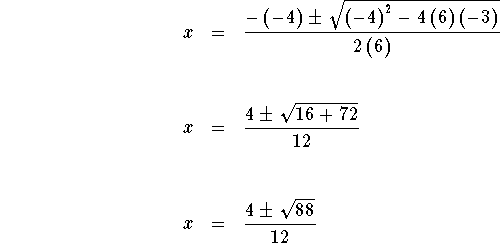
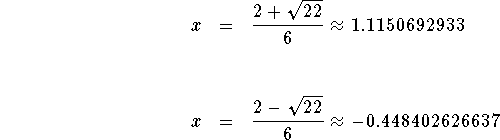
The answers are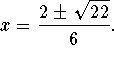 
However, this may or may not
be the answer. You must check the solution with the original equation.
Check the solution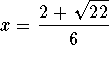 
by substituting 1.1150692933
in the original equation for x. If the left side of the equation equals the
right side of the equation after the substitution, you have found the
correct answer.
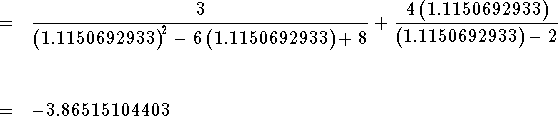
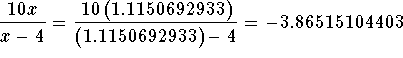
Since the left side of the original equation is equal to the right side of the original equation after we substitute the value 1.1150692933 for x, then x=1.1150692933 is a solution.
Check the solution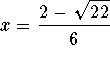 
by substituting
-0.448402626637 in the original equation for x. If the left side of the
equation equals the right side of the equation after the substitution, you
have found the correct answer.
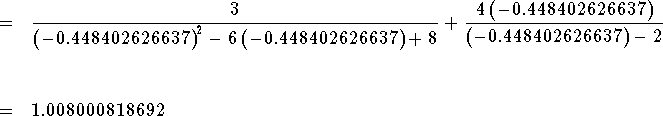
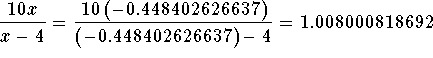
Since the left side of the original equation is equal to the right side of the original equation after we substitute the value -0.448402626637 for x, then x=-0.448402626637 is a solution.
You can also check your answer by graphing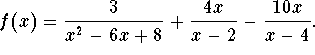 
(formed by subtracting the right
side of the original equation from the left side). Look to see where the
graph crosses the x-axis; that will be the real solution. Note that the
graph crosses the x-axis at two places: 
.
We have verified the solution two ways.
If you would like to go back to the equation table of contents, click on contents.
This site was built to accommodate the needs of students. The topics and problems are what students ask for. We ask students to help in the editing so that future viewers will access a cleaner site. If you feel that some of the material in this section is ambiguous or needs more clarification, please let us know by e-mail.
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.
