 EQUATIONS INVOLVING
FRACTIONS (RATIONAL EQUATIONS)
EQUATIONS INVOLVING
FRACTIONS (RATIONAL EQUATIONS)
 EQUATIONS INVOLVING
FRACTIONS (RATIONAL EQUATIONS)
EQUATIONS INVOLVING
FRACTIONS (RATIONAL EQUATIONS)

Note:
If you would like an in-depth review of fractions, click on Fractions.
Solve for x in the following equation.
Problem 5.4 b:
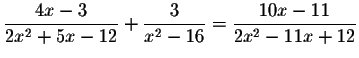
Answer: The exact answers are
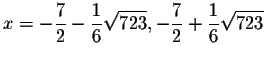
The approximate answers are
![]()
Solution:
Rewrite the equation such that all the denominators are factored:
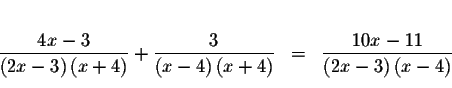
Recall that you cannot divide by zero. Therefore, the first fraction is
valid if ,
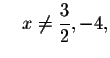 the second fraction is valid
if
the second fraction is valid
if
![]() and the third fraction is valid is
and the third fraction is valid is
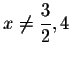 . If
. If
![]() or -4 turn out to be the
solutions, you must discard them as extraneous solutions.
or -4 turn out to be the
solutions, you must discard them as extraneous solutions.
Multiply both sides of the equation by an expression that represents the
lowest common denominator. The expression
![]() is the smallest expression because it is the
smallest expression that is divisible by all three denominators.
is the smallest expression because it is the
smallest expression that is divisible by all three denominators.
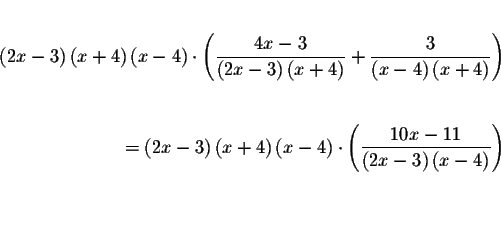
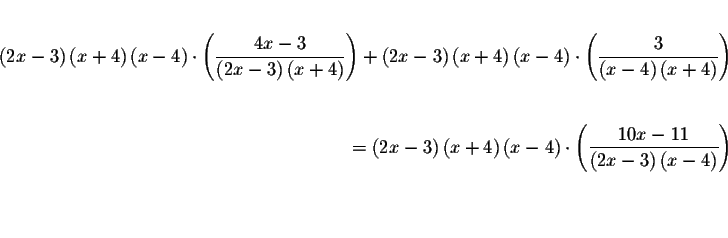
This equation can be written as
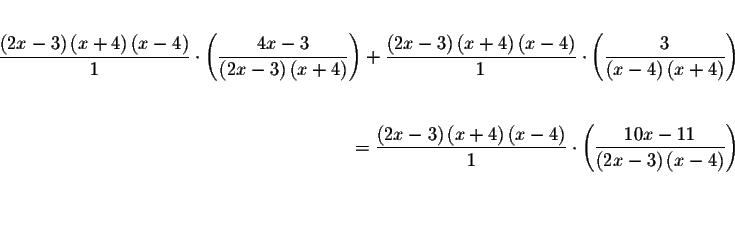
Multiply the fractions where indicated.
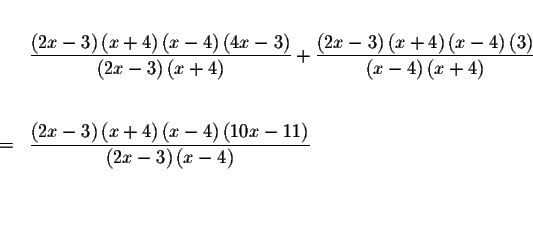
Rearrange the factors in the numerators and rewrite the equations as
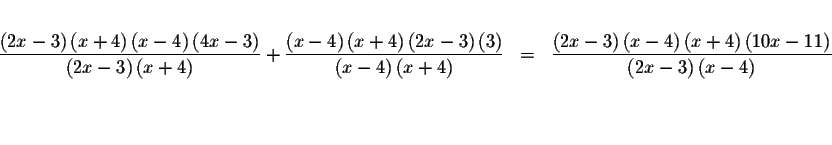
Rewrite the equation once again as
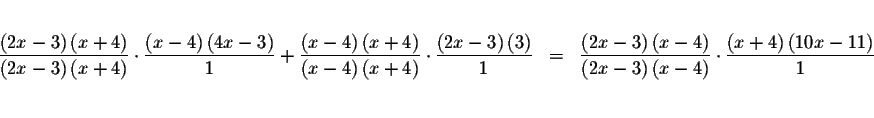
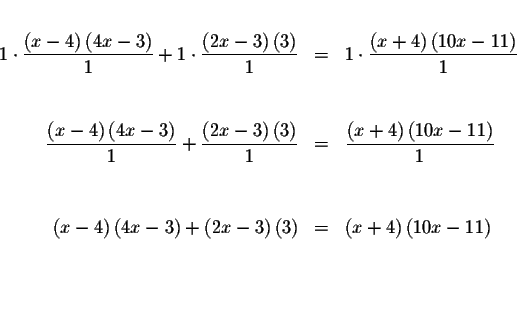
Simplify the last equation and solve for x.
![\begin{eqnarray*}&& \\
\left( x-4\right) \left( 4x-3\right) +\left( 2x-3\right)...
...\left[ \left( x+4\right) \left(
10x-11\right) \right] \\
&& \\
\end{eqnarray*}](img19.gif)
![\begin{eqnarray*}&& \\
\left[ 4x^{2}-19x+12\right] +\left[ 6x-9\right] &=&\left...
...x-44 \\
&& \\
&& \\
4x^{2}-13x+3 &=&10x^{2}+29x-44 \\
&& \\
\end{eqnarray*}](img20.gif)
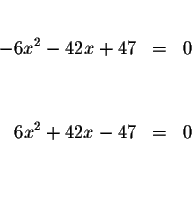
6x2+42x-47=0 when
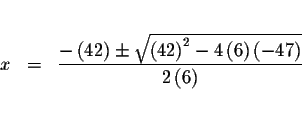
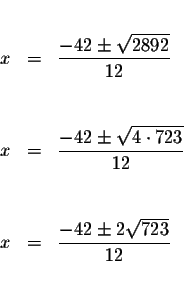
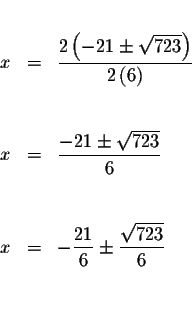
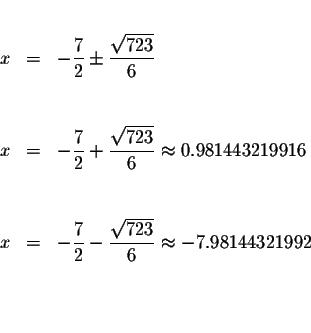
There are two real solutions:
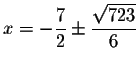
Check the two answers in the original equation.
Check the solution
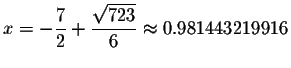 by substituting
0.981443219916 in the original equation
for x. If the left side of the equation equals the right side of the
equation after the substitution, you have found the correct answer.
by substituting
0.981443219916 in the original equation
for x. If the left side of the equation equals the right side of the
equation after the substitution, you have found the correct answer.
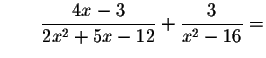

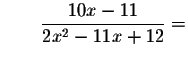

Since the left side of the original equation is not equal to the right side of the original equation after we substitute the value 0.981443219916 for x, then x=0.981443219916 is a solution.
Check the solution
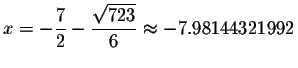 by substituting
-7.98144321992 in the original equation
for x. If the left side of the equation equals the right side of the
equation after the substitution, you have found the correct answer.
by substituting
-7.98144321992 in the original equation
for x. If the left side of the equation equals the right side of the
equation after the substitution, you have found the correct answer.
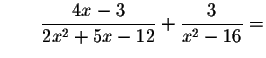

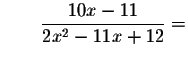
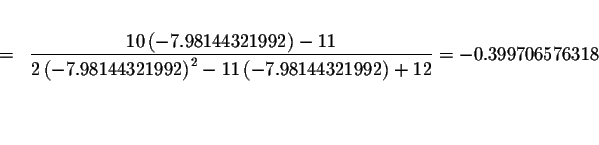
Since the left side of the original equation is not equal to the right side of the original equation after we substitute the value -7.98144321992for x, then x=-7.98144321992 is a solution.
You can also check your answer by graphing
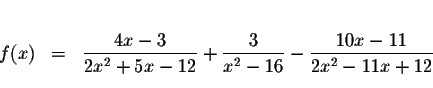
This means that there are two real solutions and the solutions are x=3,5.
If you would like to go back to the equation table of contents, click on contents.
This site was built to accommodate the needs of students. The topics and problems are what students ask for. We ask students to help in the editing so that future viewers will access a cleaner site. If you feel that some of the material in this section is ambiguous or needs more clarification, please let us know by e-mail.

Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.
