EQUATIONS INVOLVING FRACTIONS (RATIONAL EQUATIONS)

Note:

• A rational equation is an equation where at least one denominator contains a variable.

• When a denominator contains a variable, there is a restriction on the domain. The variable cannot take on any number that would cause any denominator to be zero.

• The first step is solving a rational equation is to convert the equation to an equation without denominators. This new equation may be equivalent (same solutions as the original equation) or it may not be equivalent (extraneous solutions).

• The next step is to set the equation equal to zero and solve.

• Remember that you are trying to isolate the variable.

• Depending on the problem, there are several methods available to help you solve the problem.

If you would like an in-depth review of fractions, click on Fractions.

Solve for x in the following equation.

Problem 5.5 b:         $$\frac{10}{x^{2}-6x+5}+6=2x-4$$

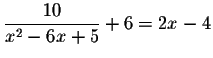
Answer:     $x=6,\ x=\displaystyle \frac{5\pm \sqrt{5}}{2}\bigskip\bigskip$

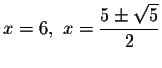
Simplify the equation by subtracting 6 from both sides of the equation.

$$\begin{eqnarray*}&& \\ \displaystyle \frac{10}{x^{2}-6x+5}+6 &=&2x-4 \\ && \\ ... ... && \\ \displaystyle \frac{5}{x^{2}-6x+5} &=&x-5 \\ && \\ && \end{eqnarray*}$$

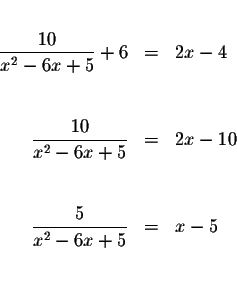
Multiply both sides of the equation by an expression that represents the lowest common denominator. The expression $\left( x^{2}-6x+5\right)$ is the smallest expression because it is the smallest expression that is divisible by all the denominators.

$$\begin{eqnarray*}&& \\ \displaystyle \frac{5}{x^{2}-6x+5} &=&x-5 \\ && \\ && ... ...\ 0 &=&\left( x-6\right) \left( x^{2}-5x+5\right) \\ && \\ && \end{eqnarray*}$$

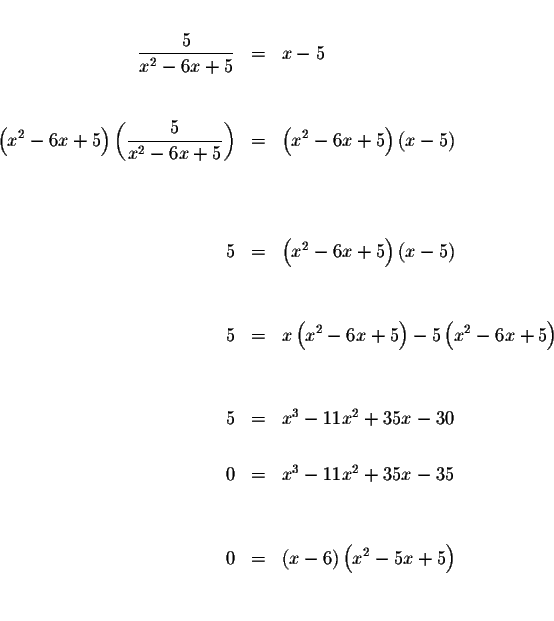
The only way a product can equal zero is if at least one of the factors equals zero.

$$\begin{eqnarray*}&& \\ If\ x-6 &=&0,\ then\ x=6 \\ && \\ If\ x^{2}-5x+5 &=&0,... ...aystyle \frac{5\pm \sqrt{5}}{2}\approx 3.618,1.382 \\ && \\ && \end{eqnarray*}$$

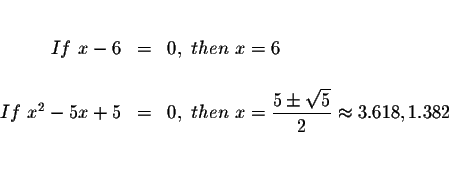
Check the answer in the original equation.

Check the solution x=6 by substituting 6 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.        

Left Side: $\qquad \displaystyle \frac{10}{x^{2}-6x+5}+6=\displaystyle \frac{10}{\left( 6\right) ^{2}-6\left( 6\right) +5}+6=8$

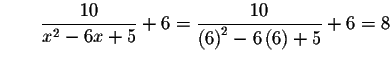
Right Side: $\qquad 2x-4=2\left( 6\right) -4=8$.

Since the left side of the original equation is equal to the right side of the original equation after we substitute the value 6 for x, then x=6 is a solution.

Check the solution x=3.618 by substituting 3.618 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.        

Left Side: $\qquad \displaystyle \frac{10}{x^{2}-6x+5}+6=\displaystyle \frac{10}{\left( 3.618\right) ^{2}-6\left( 3.618\right) +5}+6=3.236$

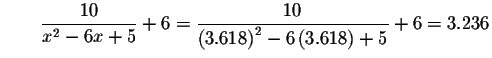
Right Side: $\qquad 2x-4=2\left( 3.618\right) -4=3.236$.

Since the left side of the original equation is equal to the right side of the original equation after we substitute the value 3.618 for x, then x=3.618 is a solution.

Check the solution x=1.382 by substituting 1.382 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.        

Left Side: $\qquad \displaystyle \frac{10}{x^{2}-6x+5}+6=\displaystyle \frac{10}{\left( 1.382\right) ^{2}-6\left( 1.382\right) +5}+6=-1.236$

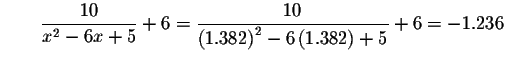
Right Side: $\qquad 2x-4=2\left( 1.382\right) -4=-1.236$

Since the left side of the original equation is equal to the right side of the original equation after we substitute the value -1.236 for x, then x=-1.236 is a solution.

You can also check your answer by graphing

$$\begin{eqnarray*}&& \\ f(x) &=&\displaystyle \frac{10}{x^{2}-6x+5}-2x+10 \\ && \end{eqnarray*}$$

(formed by subtracting the right side of the original equation from the left side). Look to see where the graph crosses the x-axis; that will be the real solution. Note that the graph crosses the x-axis at three spots, $6,\ 3.618,\ -1.236.$

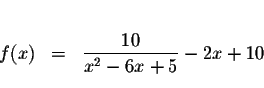
If you would like to test yourself by working some problems similar to this example, click on problem.

If you would like to go back to the equation table of contents, click on Contents

[Algebra] [Trigonometry] [Geometry] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour