SOLVING EXPONENTIAL EQUATIONS
SOLVING EXPONENTIAL EQUATIONS 
Note:
If you would like an in-depth review of exponents, the rules of exponents, exponential functions and exponential equations, click on exponential function.
Solve for the real number x in the following equation.
Problem 7.6 e:
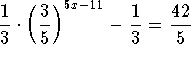
Answer:
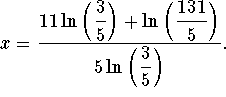
The approximate answer is
Your first objective is to isolate the term.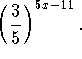 
Add 
to both sides of the equation .
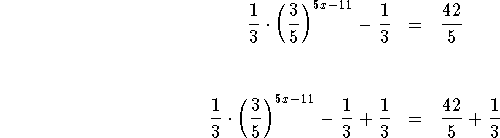
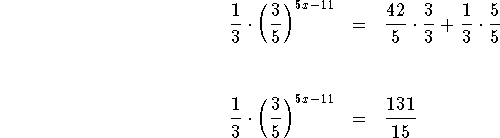
Multiply both sides of the equation by 3.
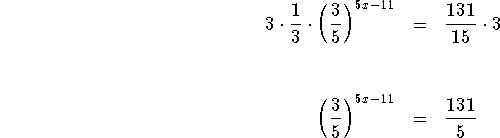
Your second objective is to isolate the variable x.
Take the natural logarithm of both sides of the equation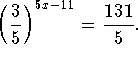 
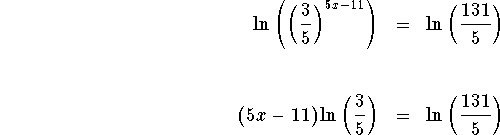
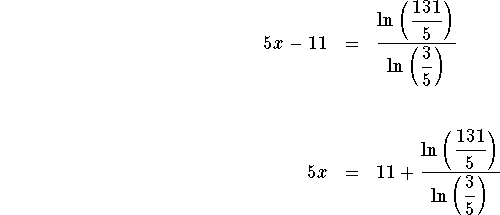
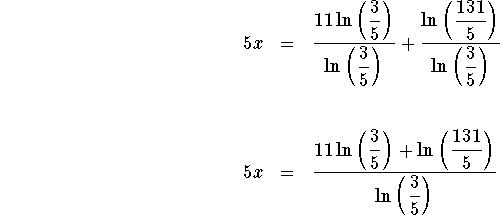
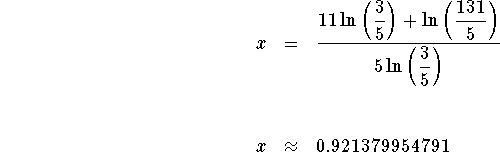
The exact answe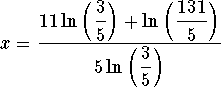r is 
and the
approximate answer is 
Check this answer in the original equation.
Check the solution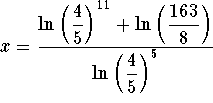 
by
substituting 
in the original equation for x. If
the left side of the equation equals the right side of the equation after
the substitution, you have found the correct answer.
for x, then 
is a solution.
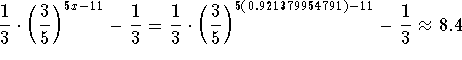
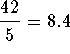
You can also check your answer by graphing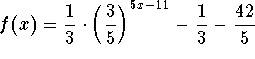 
(formed
by subtracting the right side of the original equation from the left side).
Look to see where the graph crosses the x-axis; that will be the real
solution. Note that the graph crosses the x-axis at This means that is the real
solution.
If you would like to go back to the beginning of this section, click on
Beginning
If you would like to go to the next section, click on click on
Next
If you would like to go back to the equation table of contents, click on
Contents
This site was built to accommodate the needs of students. The topics and
problems are what students ask for. We ask students to help in the editing
so that future viewers will access a cleaner site. If you feel that some of
the material in this section is ambiguous or needs more clarification,
please let us know by e-mail.
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.
