 SOLVING LOGARITHMIC EQUATIONS
SOLVING LOGARITHMIC EQUATIONS SOLVING LOGARITHMIC EQUATIONS
SOLVING LOGARITHMIC EQUATIONS
Note:
If you would like an in-depth review of logarithms, the rules of logarithms, logarithmic functions and logarithmic equations, click on logarithmic function.
Solve for x in the following equation.
Example 2:
The above equation is valid only if all the terms in the equation are valid.
The term
![]() is valid if
is valid if
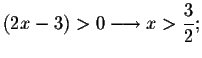 the term
the term
![]() is
valid if
is
valid if
![]() and the term
and the term
![]() is valid if x>0. The domain is the set of real numbers that are greater
than
is valid if x>0. The domain is the set of real numbers that are greater
than
![]() ,
greater than -5, and greater than 0. The domain is
therefore the set of real numbers greater than
,
greater than -5, and greater than 0. The domain is
therefore the set of real numbers greater than
![]() .
.
This is a complex equation because all the bases are different. Let's solve it first by graphing; we do this by changing all the bases to either 10 or e. Why do we change the bases to either 10 or e? Because most calculators have these functions.
Graphing Method:
Change the original equation into an equation where all the logarithmic
terms have base 10.

Rewrite the equation as
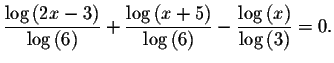
Let's call the left side of the equation f(x) and the right side of the equation g(x).
Then
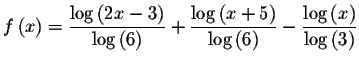 and
and
![]() Graph f(x) and g(x). We are looking for the point(s) of intersection,
Graph f(x) and g(x). We are looking for the point(s) of intersection,
![]() The solution, if any, will be the value of x in the
point(s) of intersection.
The solution, if any, will be the value of x in the
point(s) of intersection.
The graph of the right side of the equation is the set of points where the value of y equals zero. This is easy; it is the x-axis. We then look to see where the graph of f(x) crosses the x-axis.
Note that the graph only appears to the right of
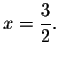 This is
consistent with our finding that the domain of the original equation is the
set of real numbers greater than
This is
consistent with our finding that the domain of the original equation is the
set of real numbers greater than
![]() .
.
The solution(s) to the original equation is(are) the set of real numbers
where f(x) crosses the x-axis (the x-intercepts are the solutions to the
problem.). You will note from the graph that f(x) crosses the x-axis at
x=1.6735161761. This means that the equation has one real solution at
![]() .
.
Algebraic Method:
Change the bases of the logarithmic terms to 10.

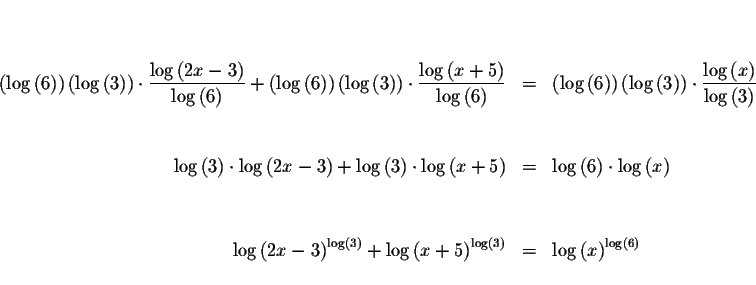
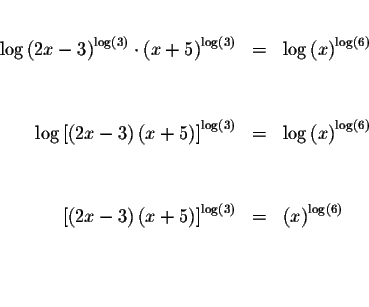
Interpolation Method:
Since the domain is the set of real numbers greater than
![]() choose numbers larger than
choose numbers larger than
![]() We will choose numbers such aand b such that f(a)>0 and f(b)<0. Somewhere between a and b, f(x) must take on the value of zero. We are looking for the value where f(x)=0.
We will choose numbers such aand b such that f(a)>0 and f(b)<0. Somewhere between a and b, f(x) must take on the value of zero. We are looking for the value where f(x)=0.
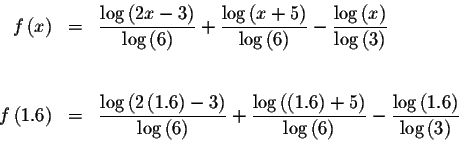

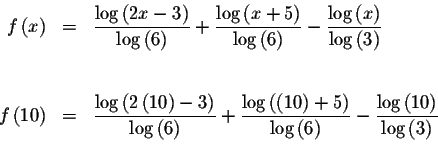

Since f(1.6)<0 and f(10)>0, we know that the graph of f(x) must cross
the x-axis between x=1.6 and x=10. This means that we know at least one
solution has a value >1.6 and <10. Since
![]() is closer to zero than
is closer to zero than
![]() ,
we know that the answer most likely lies to the left of the midpoint of 1.6and 10, or to the left of 7.4.
,
we know that the answer most likely lies to the left of the midpoint of 1.6and 10, or to the left of 7.4.
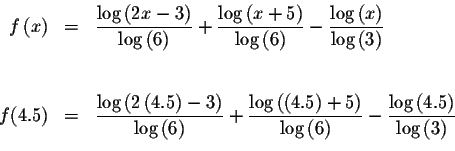
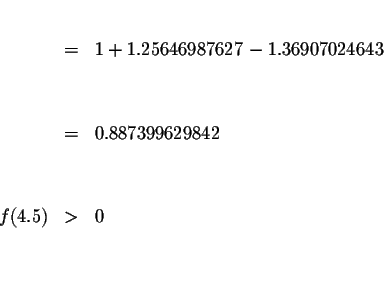
Since f(1.6)<0 and f(4.5)>0, we know that the graph of f(x) must cross
the x-axis between x=1.6 and x=4.5. This means that we know at least one
solution has a value >1.6 and <4.5. Since
![]() is closer to zero than
is closer to zero than
![]() ,
we know that the answer most likely lies to the left of the midpoint of 1.6 and 4.5 or to the left of 3.05..
,
we know that the answer most likely lies to the left of the midpoint of 1.6 and 4.5 or to the left of 3.05..
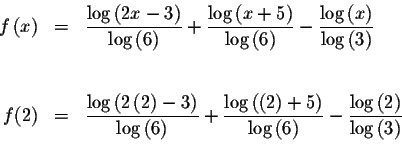
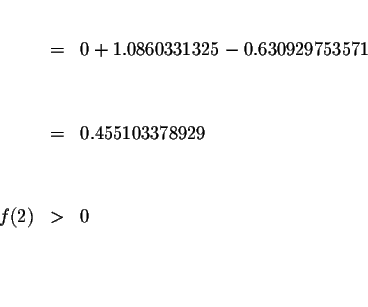
Since f(1.6)<0 and f(2)>0, we know that the graph of f(x) must cross
the x-axis between x=1.6 and x=2. This means that we know at least one
solution has a value greater than 1.6 and less than 2. Since
![]() is closer to zero than
is closer to zero than
![]() ,
we know that the answer most likely lies to the left of
the midpoint of 1.6 and 2 or to the left of 1.8.
,
we know that the answer most likely lies to the left of
the midpoint of 1.6 and 2 or to the left of 1.8.
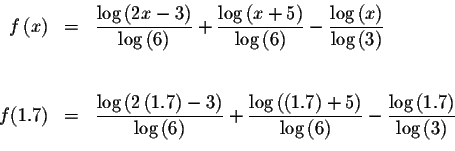

Since f(1.6)<0 and f(1.7)>0, we know that the graph of f(x) must cross
the x-axis between x=1.6 and x=1.7. This means that we know at least one
solution has a value >1.6 and <1.7. Since
![]() is closer to zero than
is closer to zero than
![]() the answer is closer to 1.7 than to 1.6.
the answer is closer to 1.7 than to 1.6.
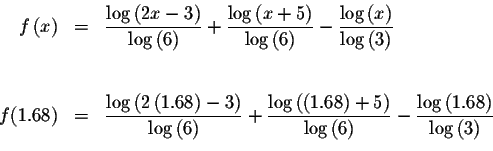

Since f(1.6)<0 and f(1.68)>0, we know that the graph of f(x) must
cross the x-axis between x=1.6 and x=1.68. This means that we know at
least one solution has a value > 1.6 and < 1.68. Since
![]() is closer to zero than
is closer to zero than
![]() the answer is closer to 1.68 than to 1.6.
the answer is closer to 1.68 than to 1.6.
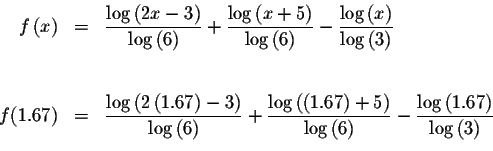
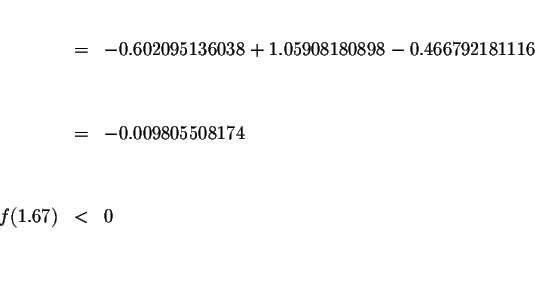
Since f(1.67)<0 and f(1.68)>0, we know that the graph of f(x) must cross the x-axis between x=1.67 and x=1.68. This means that we know at least one solution has a value greater than 1.67 and less than 1.68.
You can now try x=1.675 and place the solution between x=1.67 and x=1.675 or between x=1.675 and x=1.68. You can continue in this fashion
until your approximation of the answer is carried to as many decimals as
your problems requires. Let's try x=1.675= and evaluate f(1.675). Since we are looking for the value such that
![]() our target is 0.
our target is 0.
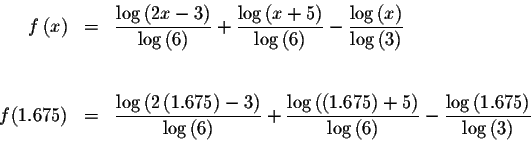

Since f(1.6)<0 and f(1.675)>0, we know that the graph of f(x) must cross the x-axis between x=1.6 and x=1.675. This means that we know at least one solution has a > 1.6 and < 1.675. How long do you keep going? To the degree of accuracy required. If your answer must be correct to three decimals places, then you keep going until the three digits to the right of the decimals in the answers are the same..
If you would like to work another example, click on example.
If you would like to test yourself by working some problems similar to this
example, click on problem.
If you would like to go to the next section, click on next.
If you would like to go back to the previous section, click on previous.
If you would like to go back to the equation table of contents, click on
contents.
This site was built to accommodate the needs of students. The topics and problems are what students ask for. We ask students to help in the editing so that future viewers will access a cleaner site. If you feel that some of the material in this section is ambiguous or needs more clarification, or you find a mistake, please let us know by e-mail.

Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.
