
 SOLVING TRIGONOMETRIC EQUATIONS
SOLVING TRIGONOMETRIC EQUATIONS

Note: If you would like a review of trigonometry, click on trigonometry.
Problem 9.10a: Solve for x in the equation
Answer: The exact answers are
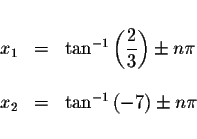
where n is an integer.
The approximate values of these solutions are
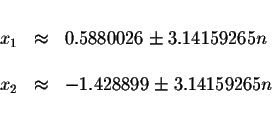
Solution:
There are an infinite number of solutions to this problem.
We can make the solution easier if we convert all the trigonometric terms to like trigonometric terms.
One common trigonometric identity is
![]() If we replace the
If we replace the
![]() term with
term with
![]() ,
all the trigonometric terms will be tangent terms.
,
all the trigonometric terms will be tangent terms.
Replace
![]() with
with
![]() in the original
equation and simplify.
in the original
equation and simplify.
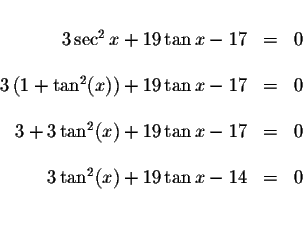
Isolate the tangent term. We can solve for ![]() by rewriting the
equation in an equivalent factored form.
by rewriting the
equation in an equivalent factored form.
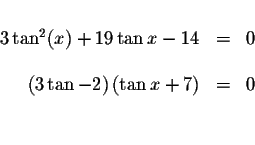
The product of two factors equals zero if at least one of the factors equals
zeros. This means that
![]() if
if ![]() or
or
![]()
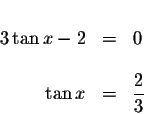
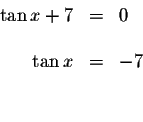
How do we isolate the x in each of these equations? We could take the inverse (arctangent) of both sides of each equation. However, the tangent function is not a one-to-one function.
Let's restrict the domain so the function is one-to-one on the restricted
domain while preserving the original range. The graph of the tangent
function is one-to-one on the interval
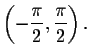 If we restrict the domain of the tangent function to that
interval , we can take the arctangent of both sides of each equation.
If we restrict the domain of the tangent function to that
interval , we can take the arctangent of both sides of each equation.
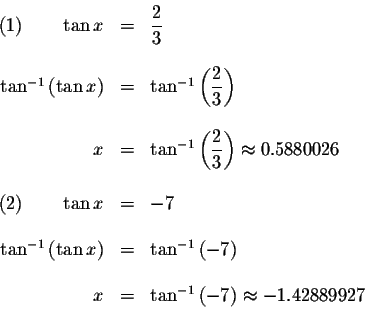
Since the period of ![]() equals
equals ![]() ,
these solutions will repeat every
,
these solutions will repeat every
![]() units. The exact solutions are
units. The exact solutions are
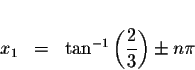
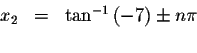
where n is an integer.
The approximate values of these solutions are
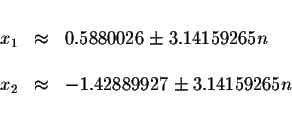
where n is an integer.
You can check each solution algebraically by substituting each solution in the original equation. If, after the substitution, the left side of the original equation equals the right side of the original equation, the solution is valid.
You can also check the solutions graphically by graphing the function formed by subtracting the right side of the original equation from the left side of the original equation. The solutions of the original equation are the x-intercepts of this graph.
Algebraic Check:
Check solution
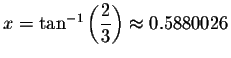
Left Side:
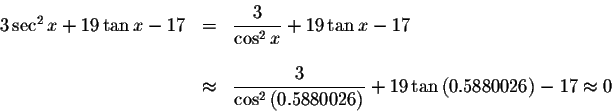
Right Side: ![]()
Since the left side of the original equation equals the right side of the original equation when you substitute 0.5880026 for x, then 0.5880026 is a solution.
Check solution
![]()
Left Side:
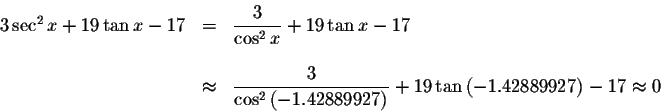
Right Side: ![]()
Since the left side of the original equation equals the right side of the original equation when you substitute -1.42889927 for x, then -1.42889927is a solution.
Graphical Check:
Graph the equation
![]() or
or
Note that the graph crosses the x-axis many times indicating many solutions. Let's check a few of these x-intercepts against the solutions we derived.
Verify the graph crosses the x-axis at
0.5880026. Since the period is
![]() ,
you can verify that the graph also crosses the
x-axis again at
0.5880026+3.14159265=3.729595 and at
,
you can verify that the graph also crosses the
x-axis again at
0.5880026+3.14159265=3.729595 and at
![]() ,
etc.
,
etc.
Verify the graph crosses the x-axis at
-1.42889927. Since the period is
![]() ,
you can verify that the graph also crosses the
x-axis again at
-1.42889927+3.14159265=1.7126934 and at
,
you can verify that the graph also crosses the
x-axis again at
-1.42889927+3.14159265=1.7126934 and at
![]() ,
etc.
,
etc.
Note: If the problem were to find the solutions in the interval
![]() ,
then you choose those solutions from the set of infinite
solutions that belong to the set
,
then you choose those solutions from the set of infinite
solutions that belong to the set
![]()
![]() 1.7126934, 3.729595, and
1.7126934, 3.729595, and
![]()
If you would like to review another solution, click on solution.
If you would like to test yourself by working some problems similar to this example, click on Problem.
If you would like to go to the next section, click on Next.
If you would like to go back to the equation table of contents, click on Contents.

