SOLVING TRIGONOMETRIC EQUATIONS

Note: If you would like a review of trigonometry, click on trigonometry.

Example 4: Solve for x in the following equation.

$\begin{displaymath}\displaystyle \displaystyle \frac{1+\cos x}{\sin x}+\displaystyle \displaystyle \frac{\sin x}{1+\cos x}=2\csc x\end{displaymath}$

There are an infinite number of solutions to this problem. There are an infinite number of solutions to this problem. Since denominators of fractions cannot equal zero, real numbers that cause the denominators to equal zero must be eliminated from the set of possible solutions. $\sin x\neq 0\rightarrow x\neq 0\pm n\pi ,\qquad$ and $\cos x\neq -1\rightarrow x\neq \pi \pm 2n\pi .$ Therefore, before we even start to solve the problem, the set of real numbers in the set $\left\{ \pm n\pi \right\}$ must be excluded from the possible set of solutions.

The equation has three different trigonometric terms. Let's manipulate the equation so that we have an equation of like trigonometric terms.

First, let's multiple the second equation by 1 in the form $\displaystyle \displaystyle \frac{1-\cos x}{% 1-\cos x},$ simplify and solve. The result will be an equation that is not equivalent to the original equation, but an equation that we can solve for x. With this type of manipulation, there may be extraneous answers. In other words, you may come up with answers for the new equation that are not solutions to the original equation. Therefore, check your answers with the original equation.

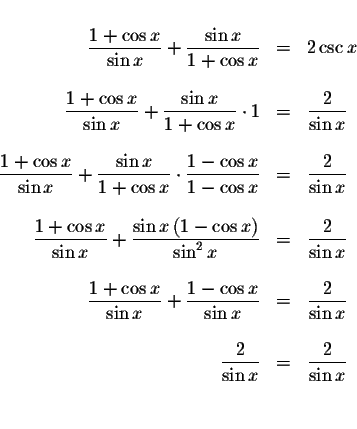
$\begin{displaymath}\begin{array}{rclll} && \\ \displaystyle \displaystyle \frac... ... x} &=&\displaystyle \frac{2}{\sin x} \\ && \\ && \end{array}\end{displaymath}$

This indicates that the solution is the set of all real numbers excluding those numbers that cause the original equation to be undefined, specific those real numbers x such that $\sin x=0$ and $\cos x+1=0.$

The set of real numbers for which $\sin x=0$ is $\left\{ 0,\pm \pi ,\pm 2\pi ,..\pm n\pi \right\}$ . The set of real numbers for which $\cos x=-1$ is $% \left\{ ,\pm \pi ,\pm 3\pi ,..\pm \left( 2n+1\right) \pi \right\}$ . The solution to this problem is the set of real numbers except those numbers in the set $\left\{ 0,\pm \pi ,\pm 2\pi ,..\pm n\pi \right\} .$

where n is an integer.

You can check each solution algebraically by substituting any real number, except real numbers in the excluded set, in the original equation. If, after the substitution, the left side of the original equation equals the right side of the original equation, the solution is valid.

You can also check the solutions graphically by graphing the function formed by subtracting the right side of the original equation from the left side of the original equation. The solutions of the original equation are the x-intercepts of this graph.

Algebraic Check:

Choose any real number, say x=7, other than the excluded numbers to illustrate that it will check as a solution.

Left Side:

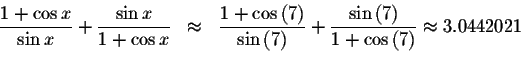
$\begin{displaymath}\begin{array}{rclll} \displaystyle \displaystyle \frac{1+\cos... ... }{1+\cos \left( 7\right) }\approx 3.0442021 \\ && \end{array}\end{displaymath}$

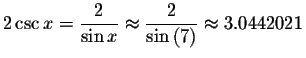
Right Side: $2\csc x=\displaystyle \displaystyle \frac{2}{\sin x}\approx \displaystyle \displaystyle \frac{2}{\sin \left( 7\right) }\approx 3.0442021\bigskip$

This indicates that 7 is a solution. You could keep trying thousands of random numbers and they will all check out.

Graphical Check:

Graph the equation 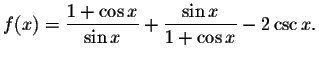$f(x)=\displaystyle \displaystyle \frac{1+\cos x}{\sin x}+\displaystyle \displaystyle \frac{\sin x}{1+\cos x}% -2\csc x.$ Note that the graph is the x-axis indicating that it crosses the x-axis everywhere except for those numbers in the excluded set.

If you would like to test yourself by working some problems similar to this example, click on Problem.

If you would like to go to the next section, click on Next.

If you would like to go back to the equation table of contents, click on Contents.

[Algebra] [Trigonometry] [Geometry] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]
S.O.S MATHematics home page

Author: Nancy Marcus