SOLVING TRIGONOMETRIC EQUATIONS

Note: If you would like a review of trigonometry, click on trigonometry.

Problem 9.12b: Solve for x in the equation

$\begin{displaymath}36\cos ^{4}x-25\cos ^{2}x+4=0\end{displaymath}$

Answer: The exact answers are

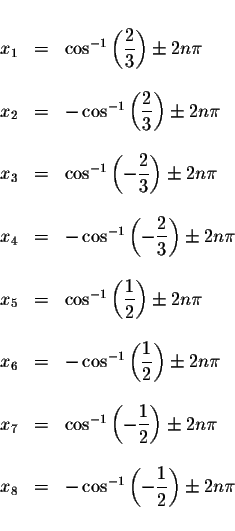
$\begin{displaymath}\begin{array}{rclll} && \\ x_{1} &=& \cos ^{-1}\left( \displ... ... -\displaystyle \frac{1}{2}\right) \pm 2n\pi \\ && \end{array}\end{displaymath}$

where n is an integer.

The approximate values of these solutions are

$\begin{displaymath}\begin{array}{rclll} && \\ x_{1} &\approx &0.84106867\pm 6.2... ... \\ x_{4} &\approx &-2.094395\pm 6.2831853n \\ && \end{array}\end{displaymath}$

$\quad$ where n is an integer.

Solution:

There are an infinite number of solutions to this problem. Let's simplify the problem by rewriting it in an equivalent factored form.

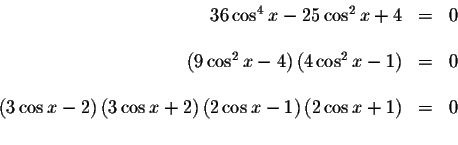
$\begin{displaymath}\begin{array}{rclll} 36\cos ^{4}x-25\cos ^{2}x+4 &=&0 \\ && ... ...\cos x-1\right) \left( 2\cos x+1\right) &=&0 \\ && \end{array}\end{displaymath}$

The only way the product equals zero is if at least one of the factors equals zero. Therefore, $36\cos ^{4}x-25\cos ^{2}x+4=0$ if $3\cos x-2=0$ , $% 3\cos x+2,$ $\cos x-1=0,$ or $\cos x+1=0.$

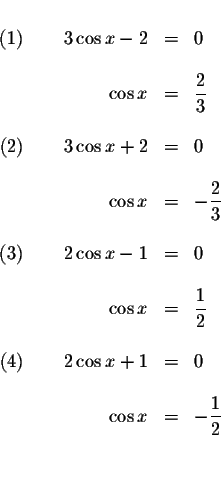
$\begin{displaymath}\begin{array}{rclll} && \\ \left( 1\right) \qquad 3\cos x-2 ... ... \cos x &=&-\displaystyle \frac{1}{2} \\ && \\ && \end{array}\end{displaymath}$

How do we isolate the x in each of these equations? We could take the inverse (arccosine) of both sides of the equation. However, the cosine function is not a one-to-one function.

Let's restrict the domain so the function is one-to-one on the restricted domain while preserving the original range. The cosine function is one-to-one on the interval $\left[ 0,\pi \right] .$ If we restrict the domain of the cosine function to that interval , we can take the arccosine of both sides of each equation.

$\begin{displaymath}\begin{array}{rclll} \left( 1\right) \qquad \cos x_{1} &=&\di... ... \frac{1}{2}\right) \approx 2.0943951 \\ && \\ && \end{array}\end{displaymath}$

We know that $\cos x=\cos \left( -x\right) .\$ Therefore,
If $\cos x =\displaystyle \frac{2}{3}$ , then

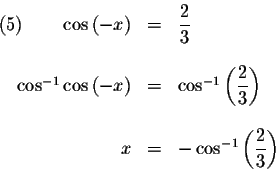
$\begin{displaymath}\begin{array}{rclll} \left( 5\right) \qquad \cos \left( -x\ri... ...os ^{-1}\left( \displaystyle \frac{2}{3}\right) \\ \end{array}\end{displaymath}$

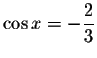If $\cos x =-\displaystyle \frac{2}{3}$ , then

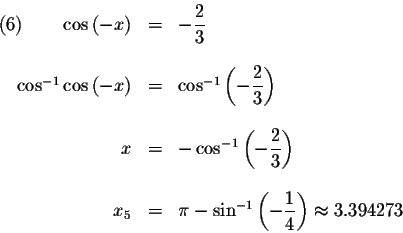
$\begin{displaymath}\begin{array}{rclll} \left( 6\right) \qquad \cos \left( -x\ri... ...isplaystyle \frac{1}{4}\right) \approx 3.394273 \\ \end{array}\end{displaymath}$

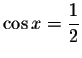If $\cos x = \displaystyle \frac{1}{2}$ , then

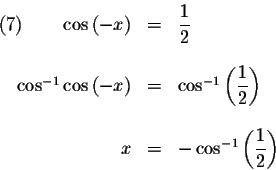
$\begin{displaymath}\begin{array}{rclll} \left( 7\right) \qquad \cos \left( -x\ri... ...os ^{-1}\left( \displaystyle \frac{1}{2}\right) \\ \end{array}\end{displaymath}$

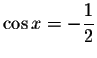If $\cos x = -\displaystyle \frac{1}{2}$ , then

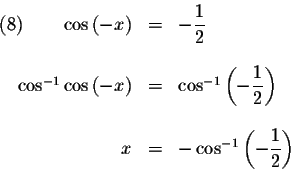
$\begin{displaymath}\begin{array}{rclll} \left( 8\right) \qquad \cos \left( -x\ri... ...{-1}\left( -\displaystyle \frac{1}{2}\right) \\ && \end{array}\end{displaymath}$

Since the period of $\cos x$ equals $2\pi$ , these solutions will repeat every $2\pi$ units. The exact solutions are

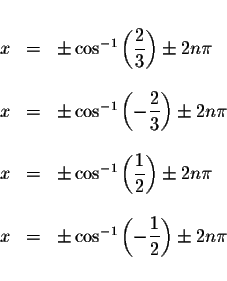
$\begin{displaymath}\begin{array}{rclll} && \\ x &=&\pm \cos ^{-1}\left( \displa... ... -\displaystyle \frac{1}{2}\right) \pm 2n\pi \\ && \end{array}\end{displaymath}$

where n is an integer.

The approximate values of these solutions are

$\begin{displaymath}\begin{array}{rclll} && \\ x &\approx &0.84106867\pm 6.28318... ... && \\ x &\approx &2.0943951\pm 6.2831853n \\ && \end{array}\end{displaymath}$

where n is an integer.

You can check each solution algebraically by substituting each solution in the original equation. If, after the substitution, the left side of the original equation equals the right side of the original equation, the solution is valid.

You can also check the solutions graphically by graphing the function formed by subtracting the right side of the original equation from the left side of the original equation. The solutions of the original equation are the x-intercepts of this graph.

Algebraic Check:

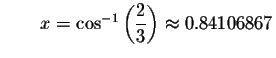
Check solution $\qquad x= \cos ^{-1}\left( \displaystyle \displaystyle \frac{2}{3}\right) \approx 0.84106867$

Left Side:

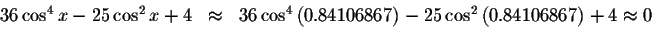
$\begin{displaymath}\begin{array}{rclll} 36\cos ^{4}x-25\cos ^{2}x+4 &\approx &36... ...cos ^{2}\left( 0.84106867\right) +4\approx 0 \\ && \end{array}\end{displaymath}$

Right Side: $0\bigskip$

Since the left side of the original equation equals the right side of the original equation when you substitute 0.84106867 for x, then 0.84106867is a solution.

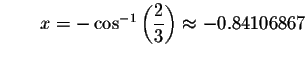
Check solution $\qquad x=- \cos ^{-1}\left( \displaystyle \displaystyle \frac{2}{3}\right) \approx -0.84106867$

Left Side:

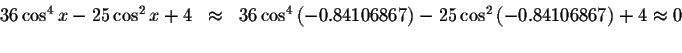
$\begin{displaymath}\begin{array}{rclll} 36\cos ^{4}x-25\cos ^{2}x+4 &\approx &36... ...os ^{2}\left( -0.84106867\right) +4\approx 0 \\ && \end{array}\end{displaymath}$

Right Side: $0\bigskip$

Since the left side of the original equation equals the right side of the original equation when you substitute -0.84106867 for x, then -0.84106867is a solution.

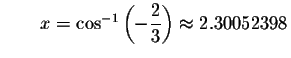
Check solution $\qquad x= \cos ^{-1}\left( -\displaystyle \displaystyle \frac{2}{3}\right) \approx 2.30052398$

Left Side:

$\begin{displaymath}\begin{array}{rclll} 36\cos ^{4}x-25\cos ^{2}x+4 &\approx &36... ...cos ^{2}\left( 2.30052398\right) +4\approx 0 \\ && \end{array}\end{displaymath}$

Right Side: $0\bigskip$

Since the left side of the original equation equals the right side of the original equation when you substitute 2.30052398 for x, then 2.30052398is a solution.

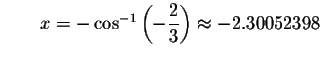
Check solution $\qquad x=- \cos ^{-1}\left( -\displaystyle \displaystyle \frac{2}{3}\right) \approx -2.30052398$

Left Side:

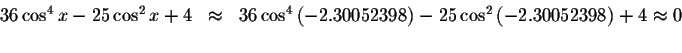
$\begin{displaymath}\begin{array}{rclll} 36\cos ^{4}x-25\cos ^{2}x+4 &\approx &36... ...os ^{2}\left( -2.30052398\right) +4\approx 0 \\ && \end{array}\end{displaymath}$

Right Side: $0\bigskip$

Since the left side of the original equation equals the right side of the original equation when you substitute -2.30052398 for x, then -2.30052398is a solution.

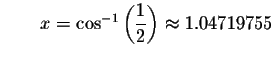
Check solution $\qquad x= \cos ^{-1}\left( \displaystyle \displaystyle \frac{1}{2}\right) \approx 1.04719755$

Left Side:

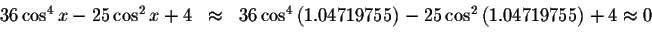
$\begin{displaymath}\begin{array}{rclll} 36\cos ^{4}x-25\cos ^{2}x+4 &\approx &36... ...cos ^{2}\left( 1.04719755\right) +4\approx 0 \\ && \end{array}\end{displaymath}$

Right Side: $0\bigskip$

Since the left side of the original equation equals the right side of the original equation when you substitute 1.04719755 for x, then 1.04719755is a solution.

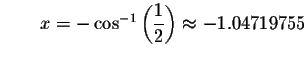
Check solution $\qquad x=- \cos ^{-1}\left( \displaystyle \displaystyle \frac{1}{2}\right) \approx -1.04719755$

Left Side:

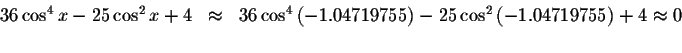
$\begin{displaymath}\begin{array}{rclll} 36\cos ^{4}x-25\cos ^{2}x+4 &\approx &36... ...os ^{2}\left( -1.04719755\right) +4\approx 0 \\ && \end{array}\end{displaymath}$

Right Side: $0\bigskip$

Since the left side of the original equation equals the right side of the original equation when you substitute -1.04719755 for x, then -1.04719755is a solution.

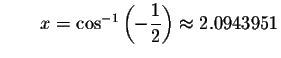
Check solution $\qquad x= \cos ^{-1}\left( -\displaystyle \displaystyle \frac{1}{2}\right) \approx 2.0943951$

Left Side:

$\begin{displaymath}\begin{array}{rclll} 36\cos ^{4}x-25\cos ^{2}x+4 &\approx &36... ...\cos ^{2}\left( 2.0943951\right) +4\approx 0 \\ && \end{array}\end{displaymath}$

Right Side: $0\bigskip$

Since the left side of the original equation equals the right side of the original equation when you substitute 2.0943951 for x, then 2.0943951 is a solution.

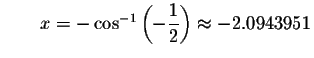
Check solution $\qquad x=- \cos ^{-1}\left( -\displaystyle \displaystyle \frac{1}{2}\right) \approx -2.0943951$

Left Side:

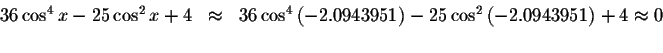
$\begin{displaymath}\begin{array}{rclll} 36\cos ^{4}x-25\cos ^{2}x+4 &\approx &36... ...cos ^{2}\left( -2.0943951\right) +4\approx 0 \\ && \end{array}\end{displaymath}$

Right Side: $0\bigskip$

Since the left side of the original equation equals the right side of the original equation when you substitute -2.0943951 for x, then -2.0943951is a solution.

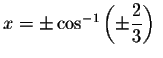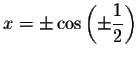We have just verified algebraically that the exact solutions are $x=\pm \cos ^{-1}\left( \pm \displaystyle \displaystyle \frac{2}{3}\right) \$ and $x=\pm \cos \left( \pm \displaystyle \displaystyle \frac{1}{2% }\right)$ and these solutions repeat every $\pm 2\pi$ units.

The approximate values of these solutions are $x\approx \pm 0.84106867$ , $\pm 2.30052397$ , $\pm 1.04719755\$ and $\pm 2.0943951$ and these solutions repeat every $\pm 6.2831853$ units.

Graphical Check:

Graph the function $f(x)=36\cos ^{4}x-25\cos ^{2}x+4$ , formed by subtracting the right side of the original equation from the left side of the original equation. The x-intercepts are the real solutions.

Note that the graph crosses the x-axis many times indicating many solutions. Check the x-intercepts of the graph to see if they match the solutions.

If you would like to review the solution of another problem, click on solution.

If you would like to go back to the equation table of contents, click on Contents.

[Algebra] [Trigonometry] [Geometry] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]
S.O.S MATHematics home page

Author: Nancy Marcus