SOLVING TRIGONOMETRIC EQUATIONS


Note:

If you would like an review of trigonometry, click on trigonometry.


Solve for x in the following equation.


Example 4:

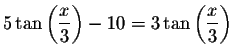
$5\tan \left( \displaystyle \frac{x}{3}\right) -10=3\tan \left( \displaystyle \frac{x }{3}\right) $



There are an infinite number of solutions to this problem. To solve for x, you must first isolate the tangent term.

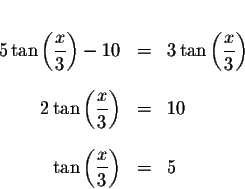
\begin{eqnarray*}&& \\ 5\tan \left( \displaystyle \frac{x}{3}\right) -10 &=&3\t... ...&10 \\ && \\ \tan \left( \displaystyle \frac{x}{3}\right) &=&5 \end{eqnarray*}


If we restriction the domain of the tangent function to 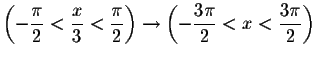$\left( -\displaystyle \frac{\pi }{2}<\displaystyle \frac{x}{3}<\displaystyle \... ... \left( -\displaystyle \frac{3\pi }{2} <x<\displaystyle \frac{3\pi }{2}\right) $, we can use the inverse tangent function to solve for reference angle $x^{\prime }$ and then x.

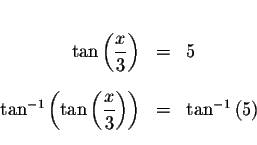
\begin{eqnarray*}&& \\ \tan \left( \displaystyle \frac{x}{3}\right) &=&5 \\ &&... ...e \frac{x}{3}\right) \right) &=&\tan ^{-1}\left( 5\right) \\ && \end{eqnarray*}
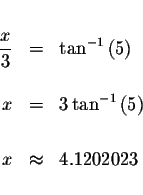
\begin{eqnarray*}&&\\ \displaystyle \frac{x}{3} &=&\tan ^{-1}\left( 5\right) \\... ...tan ^{-1}\left( 5\right) \\ && \\ x &\approx &4.1202023 \\ && \end{eqnarray*}
\begin{eqnarray*}\mbox{ Reference Angle } &:&x^{\prime }\approx 3\tan ^{-1}\left... ...nce Angle } &:&x^{\prime }\approx 4.1202023 \\ && \\ && \\ && \end{eqnarray*}


The solution is $x=3\tan ^{-1}\left( 5\right) .\bigskip\bigskip\bigskip $

The period of the tangent function is $\pi $ and the period of this function is $3\pi .$ This means that the values will repeat every $3\pi $ radians in both directions. Therefore, the exact solutions are $x=3\tan ^{-1}\left( 5\right) \pm n\left( 3\pi \right) $ n is an integer.


The approximate solutions are $x\approx 4.1202023\pm n\left( 3\pi \right) .$



These solutions may or may not be the answers to the original problem. You much check them, either numerically or graphically, with the original equation.



Numerical Check:


Check answer x=4.1202023


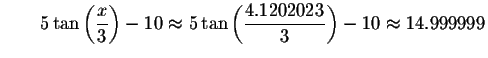
Since the left side equals the right side when you substitute 4.1202023for x, then 4.1202023 is a solution.




Check answer $x=4.1202023+3\pi \approx 13.54498$


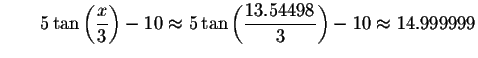
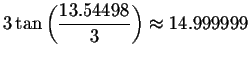
Since the left side equals the right side when you substitute 13.54498 for x, then 13.54498 is a solution.




Graphical Check:


Graph the equation 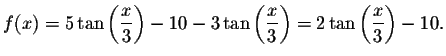$f(x)=5\tan \left( \displaystyle \frac{x}{3}\right) -10-3\tan \left( \displaystyle \frac{x}{3}\right) =2\tan \left( \displaystyle \frac{x}{3}\right) -10.$ Note that the graph crosses the x-axis many times indicating many solutions.


The graph crosses the x-axis at 4.1202023. Since the period is $3\pi \approx 9.424778$, it crosses again at 4.1202023+9.424778=13.54498 and at 4.1202023+2(9.424778)=22.969758, etc.



If you would like to test yourself by working some problems similar to this example, click on Problem.


IF you would like to go to the next section, click on Next.


If you would like to go back to the equation table of contents, click on Contents.

This site was built to accommodate the needs of students. The topics and problems are what students ask for. We ask students to help in the editing so that future viewers will access a cleaner site. If you feel that some of the material in this section is ambiguous or needs more clarification, please let us know by e-mail.

[Algebra] [Trigonometry]
[Geometry] [Differential Equations]
[Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page



Author: Nancy Marcus

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour