
 SOLVING TRIGONOMETRIC EQUATIONS
SOLVING TRIGONOMETRIC EQUATIONS

Note: If you would like a review of trigonometry, click on trigonometry.
Example 3: Solve for x in the following equation.
There are an infinite number of solutions to this problem. To solve for x, you must first isolate the sine term.

If we restrict the domain of the sine function to
![$\left[ -\displaystyle \displaystyle \frac{\pi }{2}%
\leq 2x\leq \displaystyle \...
...yle \frac{\pi }{4}\leq
x\leq \displaystyle \displaystyle \frac{\pi }{4}\right] $](img3.gif) ,
we can use the inverse sine function to
solve for reference angle
,
we can use the inverse sine function to
solve for reference angle
![]() ,
and then x. The reference angle
is always in the first quadrant and positive.
,
and then x. The reference angle
is always in the first quadrant and positive.

The
![]() has a period of
has a period of ![]() .
This means that it
makes one rotation every
.
This means that it
makes one rotation every ![]() radians. We can divide the interval
radians. We can divide the interval
![]() into four parts: quadrant I, quadrant II, quadrant III, and
quadrant IV. The sine function is positive in the first and second quadrants
and negative in the third and and fourth quadrants. In this case, one-fourth
of the rotation is
into four parts: quadrant I, quadrant II, quadrant III, and
quadrant IV. The sine function is positive in the first and second quadrants
and negative in the third and and fourth quadrants. In this case, one-fourth
of the rotation is
![]() We will use the reference angle
We will use the reference angle
![]() to find the four angles.
to find the four angles.
The first solution is the angle that terminates in the first quadrant: is
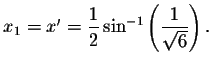 The second solution is the angle that terminates in the second quadrant:
The second solution is the angle that terminates in the second quadrant:
 .
The third solution is the angle
that terminates in the third quadrant:
.
The third solution is the angle
that terminates in the third quadrant:
 The fourth solutions is the
angle that terminates in the fourth quadrant:
The fourth solutions is the
angle that terminates in the fourth quadrant:

The period of the
![]() function is
function is ![]() This means
that the values will repeat every
This means
that the values will repeat every ![]() radians in both directions.
Therefore, the exact solutions are
radians in both directions.
Therefore, the exact solutions are
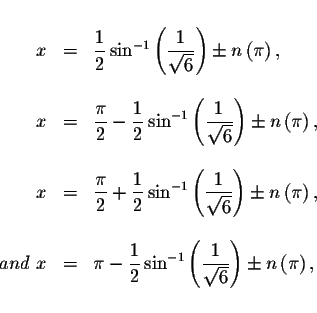
The approximate solutions are
![]()
![]() ,
,
![]() and
and
![]() where n is an
integer.
where n is an
integer.
These solutions may or may not be the answers to the original problem. You much check them, either numerically or graphically, with the original equation.
Numerical Check:
Check answer . x=0.210267
Left Side:

Right Side: ![]()
Since the left side equals the right side when you substitute 0.210267 for x, then 0.210267 is a solution.
Check answer . x=1.360529
Left Side:

Right Side: ![]()
Since the left side equals the right side when you substitute 1.360529 for x, then 1.360529 is a solution.
Check answer .x=1.78106
Left Side:

Right Side: ![]()
Since the left side equals the right side when you substitute 1.78106 for x, then 1.78106 is a solution.
Check answer .x=2.93133
Left Side:

Right Side: ![]()
Since the left side equals the right side when you substitute 2.93133 for x, then 2.93133 is a solution.
Graphical Check:
Graph the equation
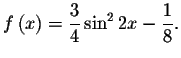 Note that the graph crosses the x-axis many times indicating many solutions.
Note that the graph crosses the x-axis many times indicating many solutions.
Note that it crosses four times in the interval from 0 ro
![]() ,
1.78106 and 2.93133.
,
1.78106 and 2.93133.
Since the period is ![]() ,
the graph crosses again at
,
the graph crosses again at
![]()
![]() ,
,
![]() ,
and
,
and
![]() etc.
etc.
If you would like to test yourself by working some problems similar to this example, click on Problem.
If you would like to go to the next section, click on Next.
If you would like to go back to the equation table of contents, click on Contents.

