SOLVING TRIGONOMETRIC EQUATIONS

Note: If you would like a review of trigonometry, click on trigonometry.

Example 4:        Solve for x in the following equation.

$$16\sec x\csc x=\sec x$$

There are an infinite number of solutions to this problem. To solve for x, set the equation equal to zero and factor.

$$\begin{array}{rclll} 16\sec x\csc x &=&\sec x \\ && \\ 16\s... ... \\ && \\ \sec x\left( 16\csc x-1\right) &=&0 \\ \end{array}$$

then

$$\begin{array}{rclll} \sec x &=&0 \\ && \\ or && \\ && \\ ... ...splaystyle \frac{1}{16} \\ && \\ \sin x &=&16 \\ \end{array}$$

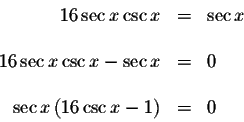
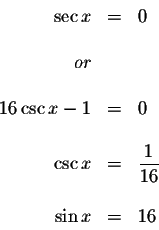
Since $\sec x\neq 0$ and $\sin x\neq 16$, there are no solutions.

Graphical Check:

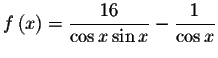Graph the equation $f(x)=16\sec x\csc x-\sec x$, formed by subtracting the right side of the original equation from the left side of the original equation. If your computer or calculator does not have these functions, graph the function $f\left( x\right) =\displaystyle \displaystyle \frac{16}{\cos x\sin x}-\displaystyle \displaystyle \frac{1}{\cos x}$. Note that the graph never crosses the x-axis indicating that there are no real solutions to this problem.

If you would like to test yourself by working some problems similar to this example, click on Problem.

If you would like to go to the next section, click on next.

If you would like to go back to the previous section, click on previous.

If you would like to go back to the equation table of contents, click on Contents.

[Algebra] [Trigonometry] [Geometry] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour