 SOLVING TRIGONOMETRIC EQUATIONS
SOLVING TRIGONOMETRIC EQUATIONS SOLVING TRIGONOMETRIC EQUATIONS
SOLVING TRIGONOMETRIC EQUATIONS
Note: If you would like a review of trigonometry, click on trigonometry.
Problem 9.5b: Solve for x in the equation
Answer: The exact answers are
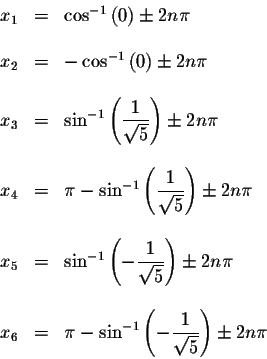
The approximate values of these solutions are
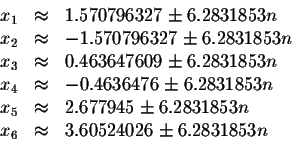
Solution:
There are an infinite number of solutions to this problem. To solve for x, set the equation equal to zero and factor.
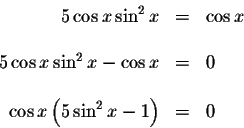
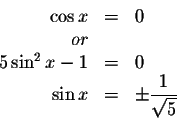
How do we isolate the x in the equations? We could take the arccosine of both sides of the cosine equation and the arcsine of both sides of the sine equations. However, the sine and cosine functions are not one-to-one functions.
Let's restrict the domain so the function is one-to-one on the restricted
domain while preserving the original range. The graph of the cosine function is one-to-one on the interval
![]() If we restrict the domain of the cosine function to that interval , we can take the arccosine of both sides of each cosine equation. The graph of the sine function is one-to-one on the interval
If we restrict the domain of the cosine function to that interval , we can take the arccosine of both sides of each cosine equation. The graph of the sine function is one-to-one on the interval
![$\left[ -\displaystyle \displaystyle \frac{\pi }{2},\displaystyle \displaystyle \frac{\pi }{2}\right] .$](img7.gif) If we restrict the domain of the sine function to that interval, we can take the arcsine of both sides of the sine equation.
If we restrict the domain of the sine function to that interval, we can take the arcsine of both sides of the sine equation.
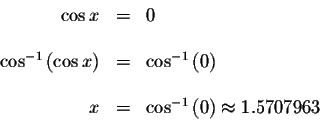
Since
![]() we know that if
we know that if ![]() then
then
![]() and
and
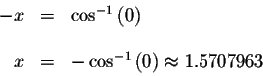
Now solve the equations
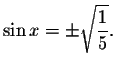 First we have
First we have
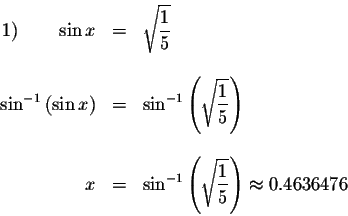
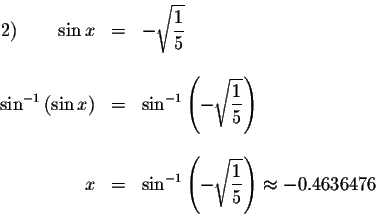
We know that
![]() Therefore, if
Therefore, if
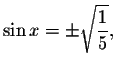 then
then
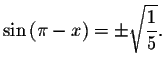 Solve the equations
Solve the equations
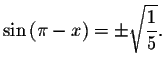
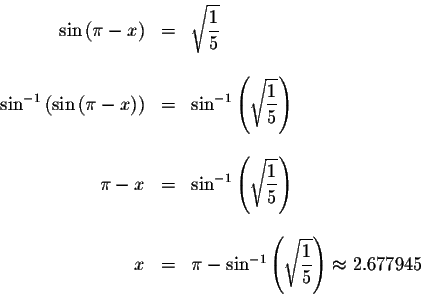
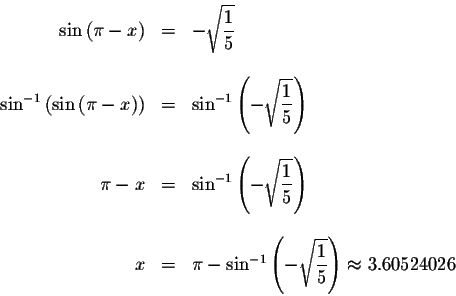
Since the period of both the cosine function and the sine function is ![]() ,
the exact solutions are
,
the exact solutions are
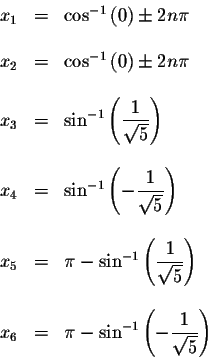
The approximate values of these solutions are
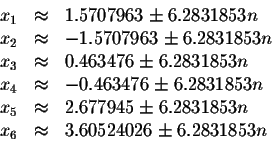
These solutions may or may not be the answers to the original problem. You much check them, either numerically or graphically, with the original equation.
Numerical Check:
Check answer
![]()
Left Side:
Right Side:
![]()
Since the left side equals the right side when you substitute 1.5707963for x, then 1.5707963 is a solution.
Check answer
![]()
Left Side:
Right Side:
![]()
Since the left side equals the right side when you substitute -1.5707963for x, then -1.5707963 is a solution.
Check answer
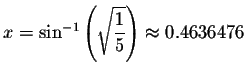
Left Side:
Right Side:
![]()
Since the left side equals the right side when you substitute 0.4636476 for x, then 0.4636476 is a solution.
Check answer
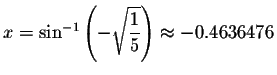
Left Side:
Right Side:
![]()
Since the left side equals the right side when you substitute -0.4636476 for x, then -0.4636476 is a solution.
Check answer
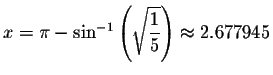
Left Side:
Right Side:
![]()
Since the left side equals the right side when you substitute 2.677945 for x, then 2.677945 is a solution.
Check answer
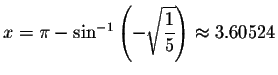
Left Side:
Right Side:
![]()
Since the left side equals the right side when you substitute 3.60524 for x, then 3.60524 is a solution.
Graphical Check:
Graph the equation
![]() Note that the graph
crosses the x-axis many times indicating many real solutions.
Note that the graph
crosses the x-axis many times indicating many real solutions.
Verify that it crosses at 1.5707963. Since the period is
![]() ,
it crosses again at
1.5707963+6.2831853=7.8539816 and at
1.5707963-6.2831853=-4.712389, etc.
,
it crosses again at
1.5707963+6.2831853=7.8539816 and at
1.5707963-6.2831853=-4.712389, etc.
Verify that it crosses at
-1.5707963. Since the period is
![]() ,
it crosses again at
-1.5707963+6.2831853=4.712389 and at
-1.5707963-6.2831853=-7.85398166, etc.
,
it crosses again at
-1.5707963+6.2831853=4.712389 and at
-1.5707963-6.2831853=-7.85398166, etc.
Verify that it crosses at 0.4636476. Since the period is
![]() ,
it crosses again at
0.4636476+6.2831853=6.7468329 and at
0.4636476-6.2831853=-5.8195376, etc.
,
it crosses again at
0.4636476+6.2831853=6.7468329 and at
0.4636476-6.2831853=-5.8195376, etc.
Verify that it crosses at
-0.4636476. Since the period is
![]() ,
it crosses again at
-0.4636476+6.2831853=5.8195377 and at
-0.4636476-6.2831853=-6.7468329, etc.
,
it crosses again at
-0.4636476+6.2831853=5.8195377 and at
-0.4636476-6.2831853=-6.7468329, etc.
Verify that it crosses at 2.677945. Since the period is
![]() ,
it crosses again at
2.677945+6.2831853=8.96113035 and at
2.677945-6.2831853=-3.60524, etc.
,
it crosses again at
2.677945+6.2831853=8.96113035 and at
2.677945-6.2831853=-3.60524, etc.
Verify that it crosses at 3.60524. Since the period is
![]() ,
it crosses again at
3.60524+6.2831853=9.88842557 and at
3.60524-6.2831853=-2.677945, etc.
,
it crosses again at
3.60524+6.2831853=9.88842557 and at
3.60524-6.2831853=-2.677945, etc.
Note: If the problem were to find the solutions in the interval
![]() ,
then you would choose those solutions from the set of
infinite solutions that belong to the set
,
then you would choose those solutions from the set of
infinite solutions that belong to the set
![]() :
:
![]() ,
and
5.8195377.
,
and
5.8195377.
If you would like to go to the next section, click on next.
If you would like to go back to the previous section, click on previous.
If you would like to go back to the equation table of contents, click on Contents.

