 SOLVING TRIGONOMETRIC EQUATIONS
SOLVING TRIGONOMETRIC EQUATIONS SOLVING TRIGONOMETRIC EQUATIONS
SOLVING TRIGONOMETRIC EQUATIONS
Note: If you would like a review of trigonometry, click on trigonometry.
Example 3: Solve for x in the following equation.
There are an infinite number of solutions to this problem.
We can make the solution process easier if we convert all the trigonometric terms to like trigonometric terms.
One common trigonometric identity is
![]() Since we
can solve for
Since we
can solve for
![]() let's
replace the
let's
replace the
![]() term in the original equation with
term in the original equation with
![]() The result is an equation equivalent to the
original equation with like trigonometric terms, in this case, sine terms.
The result is an equation equivalent to the
original equation with like trigonometric terms, in this case, sine terms.
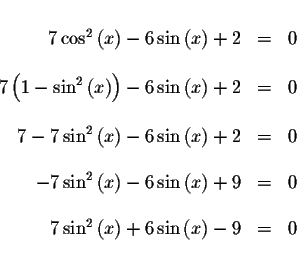
Isolate the sine term. Since this equation is not easily factored, we can
isolate the sine term by solving for
![]() using the
Quadratic Formula.
using the
Quadratic Formula.
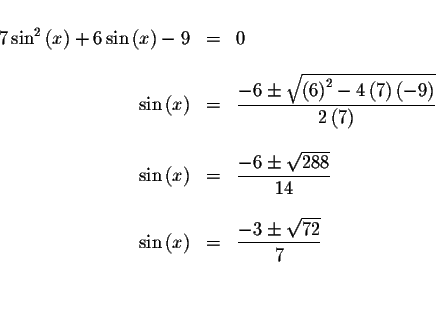
We just transformed a difficult problem into two easier problems. To find
the solution(s) to the original equation, we find the solution(s) to the
equations
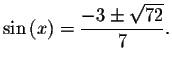
To do this we have to isolate the x. How do we isolate the x? We could take the arcsine of both sides of the equation. However, the sine function is not a one-to-one function.
Let's restrict the domain so the function is one-to-one on the restricted
domain while preserving the original range. The sine function is one-to-one
on the interval
![$\left[ -\displaystyle \displaystyle \frac{\pi }{2},\displaystyle \displaystyle \frac{\pi }{2}\right] .$](img10.gif) If we
restrict the domain of the sine function to that interval , we can take the
arcsine of both sides of each equation.
If we
restrict the domain of the sine function to that interval , we can take the
arcsine of both sides of each equation.
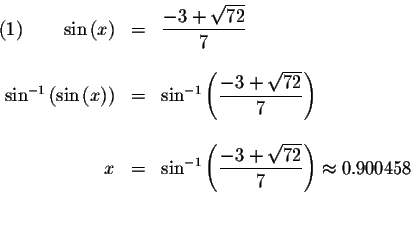
We know that
![]() Therefore,
if
Therefore,
if
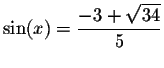 ,
then
,
then
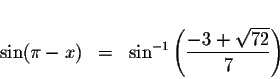
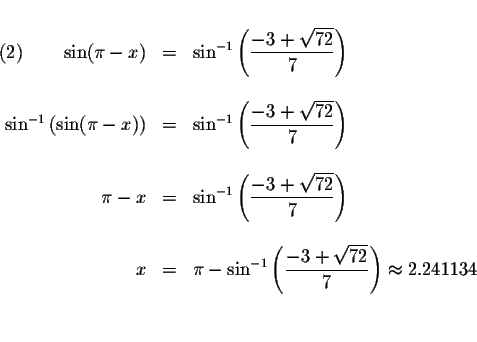
We complete the problem by solving the second equation.
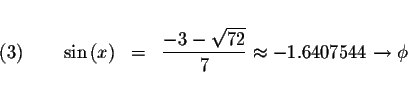
The values of
![]() range between -1 and +1 and
<tex2htmlcommentmark>
-1.6407544 is not in this range. Therefore,
range between -1 and +1 and
<tex2htmlcommentmark>
-1.6407544 is not in this range. Therefore,
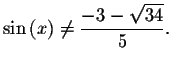
Since the period of ![]() equals
equals ![]() ,
these solutions will repeat
every
,
these solutions will repeat
every ![]() units. The exact solutions are
units. The exact solutions are
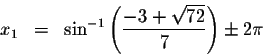
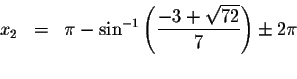
where n is an integer.
The approximate values of these solutions are
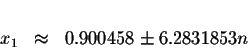
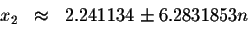
where n is an integer.
You can check each solution algebraically by substituting the solution in the original equation. If, after the substitution, the left side of the original equation equals the right side of the original equation, the solution is valid.
You can also check the solutions graphically by graphing the function formed by subtracting the right side of the original equation from the left side of the original equation. The solutions of the original equation are the x-intercepts of this graph.
Algebraic Check:
Check solution x=0.900458
Left Side:
Right Side: ![]()
Since the left side of the original equation equals the right side of the original equation when you substitute 0.900458 for x, then 0.900458 is a solution.
Check solution x=2.241134
Left Side:
Right Side: ![]()
Since the left side of the original equation equals the right side of the original equation when you substitute 2.241134 for x, then 2.241134 is a solution.
We have just verified algebraically that the exact solutions are
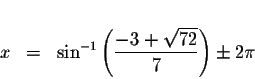
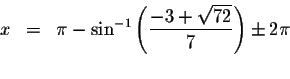
Graphical Check:
Graph the equation
![]() Note the graph crosses the x-axis many times indicating many solutions.
Let's check a few of these x-intercepts against the solutions we
derived.
Note the graph crosses the x-axis many times indicating many solutions.
Let's check a few of these x-intercepts against the solutions we
derived.
Verify the graph crosses the x-axis at 0.900458. Since the period is
![]() ,
you can verify that the graph also crosses the x-axis
again at
0.900458+6.2831853=7.1836433 and at
,
you can verify that the graph also crosses the x-axis
again at
0.900458+6.2831853=7.1836433 and at
![]() ,
etc.
,
etc.
Verify the graph crosses the x-axis at
![]() Since the period is
Since the period is
![]() ,
the graph also crosses the x-axis again at
<tex2htmlcommentmark>
2.241134+6.2831853=8.52432 and at
,
the graph also crosses the x-axis again at
<tex2htmlcommentmark>
2.241134+6.2831853=8.52432 and at
![]() ,
etc.
,
etc.
![]()
Note: If the problem were to find the solutions in the interval
![]() ,
then you choose those solutions from the set of infinite
solutions that belong to the set
,
then you choose those solutions from the set of infinite
solutions that belong to the set
![]()
![]() and
and
![]()
If you would like to test yourself by working some problems similar to this example, click on Problem.
If you would like to go to the next section, click on next.
If you would like to go back to the previous section, click on previous.
If you would like to go back to the equation table of contents, click on Contents.

