 Units of Conversion
Units of Conversion Units of Conversion
Units of Conversion

Basic to the understanding of unit conversion is the understanding of equivalence, the understanding of the multiplicative identity of 1, and how the two are related.
Equivalence:
To say that two quantities are equivalent, is to say that both quantities measure the same thing or both quantities measure the same value. For example, we could say that a person is 5 feet tall or we could say that the person is 60 inches tall. Since 5 feet and 60 inches both represent the height of the same person, these expressions are equivalent.
Most individuals would agree that there are 12 inches in 1 foot, and most have seen this relationship written as 12 inches = 1 foot. This relationship is an equation because there is an equal sign separating the left side from the right side. Does this equal sign mean that the left side of the equation is identical to the right side of the equation? Before you answer yes, let's make some observations: The number 12 and the word inches are located to the left of the equal sign, and the number 1 and the word foot are located to the right of the equal sign. Anyone can see that the left side of the equation does not look exactly like the right side of the equation. Therefore, the left and right sides of the equation are not identical.
How then can we say that the left side is equal to the right side? We can say equal without saying identical. What we are saying is that the left side is equivalent to the right side. Since the 12 inches measures the same length as does the 1 foot, the two quantities are equivalent.
Note that 1 mile is equivalent to 5,280 feet because 1 mile measures the same distance as does 5,280 feet, and the relationship can be written 1 mile = 5,280 feet. Note that 4 quarts is equivalent to 1 gallon because 4 quarts measures the same amount of liquid as does 1 gallon, and the relationship can be written 4 quarts = 1 gallon.
Multiplicative identity of 1:
In the real number system, the multiplicative identity is 1. This means that you can multiply any real number by 1 and not change the original number. For example,
 , and
, and
![]() .
.
Since division is another form of multiplication, we can also divide an expression by 1 without changing the value of the original number. For example,
 , and
, and
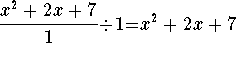 .
.
When we combine the concept of equivalence with the multiplicative identity, we have a powerful tool, a tool that is used in unit conversion. We use the concept of equivalence to show that the number 1 has many faces.
We know that a fraction has a value of 1 when the numerator equals the denominator. Now we can say that a fraction has a value of 1 when the numerator and denominator are equivalent.
Let's illustrate how this works. If we divide both sides of the equation ![]() by
by ![]() , we have the new equation
, we have the new equation  . Note that the fraction has a value of 1 and the numerator
and denominator are not identical. However, the numerator and
denominator are equivalent because they measure the same thing.
. Note that the fraction has a value of 1 and the numerator
and denominator are not identical. However, the numerator and
denominator are equivalent because they measure the same thing.
This review will provide examples and problems for various topics of units of conversion.
Back to the Main Menu.
If you have forgotten how to manipulate fractions, visit Fractions for Adults on SOSMath.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus