 Techniques of Differentiation - Exercise 1
Techniques of Differentiation - Exercise 1
 Techniques of Differentiation - Exercise 1
Techniques of Differentiation - Exercise 1
Exercise 1. Find the derivative of the function
Answer. We use the quotient rule. We have
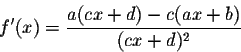
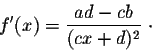
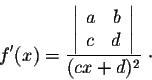
 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Mohamed A. Khamsi