Techniques of Differentiation - Exercise 2

Exercise 2. Find the derivative of

$$f(x) = \frac{\sqrt{x}}{x^2 - x + 3}$$

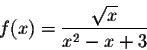
Answer. We will use the quotient rule to get

$$f'(x) = \frac{(\sqrt{x})' (x^2 - x+3) - (2x - 1)\sqrt{x}}{(x^2 - x + 3)^2}\cdot$$

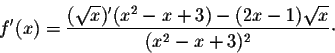
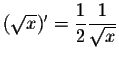Since $(\sqrt{x})' = \displaystyle \frac{1}{2} \frac{1}{\sqrt{x}}$, we get

$$(\sqrt{x})' (x^2 - x+3) - (2x - 1)\sqrt{x}= -\frac{3}{2} x\sqrt{x} + \frac{\sqrt{x}}{2} + \frac{3}{2\sqrt{x}} \cdot$$

Putting things together one will get f '(x).

[Back] [Next] [Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Complex Variables] [Matrix Algebra]

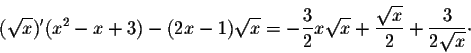
S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour