 Techniques of Differentiation - Exercise 4
Techniques of Differentiation - Exercise 4
Exercise 4. Find the points on the graph of
y = x3/2 -
x1/2 at which the tangent line is parallel to the line y+2x
= 1. Also find the points on the same graph at which the
tangent line is perpendicular to the line y-x = 3.
Answer. First let us find the points on the graph at which
the tangent line is parallel to the line y+2x = 1. For that,
we need the slope of any tangent line which is given by the
derivative
We know that two lines are parallel if and only if they have the
same slope. Since the slope of the line y+2x = 1 is -2, we
then are left to solve
We rewrite this equation to get
which is a quadratic equation in  .
Therefore we must
have
.
Therefore we must
have
Since  has to be non-negative, we have to discard the
negative solution and are thus left with
has to be non-negative, we have to discard the
negative solution and are thus left with
or equivalently
So there is only one point on the graph at which the tangent line
is parallel to the line y+2x = 1.
Next we look for the points on the graph at which the tangent
line is perpendicular to the line y-x = 3. In this case, the
slope of tangent line should be
As before we must solve the equation
We rewrite this equation to get
Therefore
which implies
 or
equivalently
or
equivalently
This is the only point on the graph at which the tangent line is
perpendicular to the line y-x = 3.
[Back]
[Next]
[Trigonometry]
[Calculus]
[Geometry]
[Algebra]
[Differential Equations]
[Complex Variables]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.
Mohamed A. Khamsi
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 Techniques of Differentiation - Exercise 4
Techniques of Differentiation - Exercise 4
 Techniques of Differentiation - Exercise 4
Techniques of Differentiation - Exercise 4
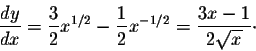



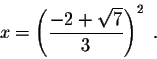



 or
equivalently
or
equivalently
 S.O.S MATHematics home page
S.O.S MATHematics home page