 Global Extrema
Global Extrema
 Global Extrema
Global Extrema
On the last page you learned how to find local extrema; one is often more interested in finding global extrema:
We say that the function f(x) has a global maximum at
x=x0 on the interval I, if
![]() for all
for all ![]() .
Similarly, the function f(x) has a global minimum
at x=x0 on the interval I, if
.
Similarly, the function f(x) has a global minimum
at x=x0 on the interval I, if
![]() for all
for all ![]() .
.
If f(x) is a continuous function on a closed bounded interval [a,b], then f(x) will have a global maximum and a global minimum on [a,b]! (This is not easy to prove, though).
On the other hand, if the interval is not bounded or closed, then
there is no guarantee that a continuous function f(x) will have
global extrema. Examples: f(x)=x2 does not have a global
maximum on the interval
![]() ,
the function
,
the function
![]() does not have a global minimum on the interval
(0,1).
does not have a global minimum on the interval
(0,1).
How can we find global extrema? Unfortunately, not every global extremum is also a local extremum:
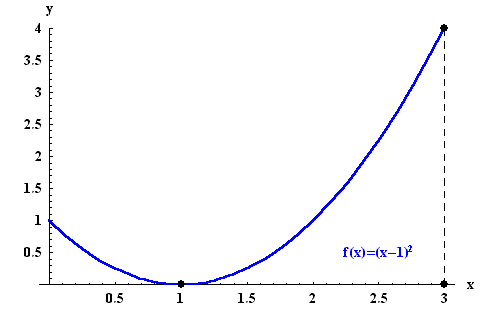
Example. Consider the function
f(x) = (x-1)2, for
![]() .
The only critical point is x=1. And the first or second
derivative test will imply that x=1 is a local minimum. Looking
at the graph (see below) we see that the right endpoint
of the interval [0,3] is the global maximum.
.
The only critical point is x=1. And the first or second
derivative test will imply that x=1 is a local minimum. Looking
at the graph (see below) we see that the right endpoint
of the interval [0,3] is the global maximum.
 |
This leads us to introduce the new concept of endpoint
extrema. Indeed, if c is an endpoint of the domain of f(x),
then f(x) is said to have an endpoint maximum at c iff
![]() for all x in the domain close to c. Similarly one
can define the concept of an endpoint minimum.
for all x in the domain close to c. Similarly one
can define the concept of an endpoint minimum.
The news is not too bad, though. If f(x) is differentiable on the interval I, then:
| Every global extremum is a local extremum or an endpoint extremum. |
This suggests the following strategy to find global extrema:
Example. Let us find the global extrema of the function f(x)=x e-x on the interval [0.1,3.5]. The function f(x)is differentiable everywhere, its derivative f'(x)=e-x-xe-x=(1-x)e-x is zero only at x=1. Thus x=1 is the only critical point. Throw in the endpoints of the interval x=0.1 and x=3.5, and evaluate f(x):
| x | f(x) | |
| 0.1 |
|
|
| 1.0 |
|
|
| 3.5 |
|
|
Thus the global minimum occurs at x=0.1, the global maximum occurs at x=1.
 |
 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Mohamed A. Khamsi