 Introduction: The Area Problem and the Definite Integral
Introduction: The Area Problem and the Definite Integral
 Introduction: The Area Problem and the Definite Integral
Introduction: The Area Problem and the Definite Integral
Integration is vital to many scientific areas. Many powerful mathematical tools are based on integration. Differential equations for instance are the direct consequence of the development of integration.
So what is integration? Integration stems from two different problems. The more immediate problem is to find the inverse transform of the derivative. This concept is known as finding the antiderivative. The other problem deals with areas and how to find them. The bridge between these two different problems is the Fundamental Theorem of Calculus.
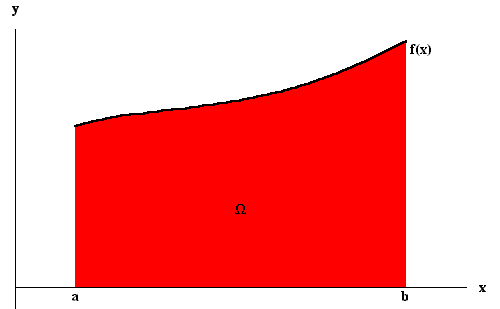
What is the "area problem"? We want to find the area of
a given region in the plane. It is not hard to see that this
problem can be reduced to finding the area of the region ![]() bounded above by the graph of a positive function f (x), bounded
below by the x-axis, bounded to the left by the vertical line
x = a, and to the right by the vertical line x = b.
bounded above by the graph of a positive function f (x), bounded
below by the x-axis, bounded to the left by the vertical line
x = a, and to the right by the vertical line x = b.
 |
The answer to this problem came through a very nice idea. Indeed,
let us split the region ![]() into small subregions which we
can approximate by rectangles or other simple geometrical figures
(whose areas we know how to compute). This is how it goes: split
the interval [a, b] into subintervals, preferably with the same
width
into small subregions which we
can approximate by rectangles or other simple geometrical figures
(whose areas we know how to compute). This is how it goes: split
the interval [a, b] into subintervals, preferably with the same
width ![]() x,
x,
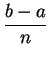 , for
i = 0, 1, ... , n - 1.
, for
i = 0, 1, ... , n - 1.
Let ![]() be the subregion bounded above by the graph of
f (x), bounded below by the x-axis, bounded to the left by
x = xi - 1, and to the right by x = xi, for
i = 1, ... , n.
Clearly we have
be the subregion bounded above by the graph of
f (x), bounded below by the x-axis, bounded to the left by
x = xi - 1, and to the right by x = xi, for
i = 1, ... , n.
Clearly we have
 |
So we focus on the subregions ![]() , for
i = 1, ... , n.
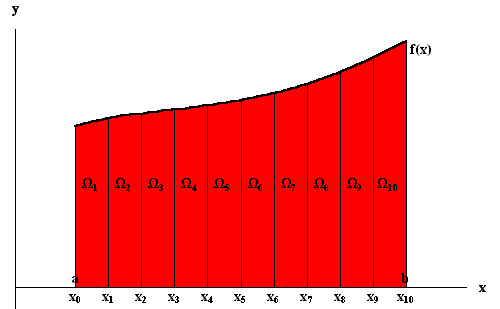
Since we want to approximate the regions by rectangles, then we
only have to worry about the upper boundary of each region (since
on the other sides we already have straight lines). Again: We are
looking for good approximations of the regions
, for
i = 1, ... , n.
Since we want to approximate the regions by rectangles, then we
only have to worry about the upper boundary of each region (since
on the other sides we already have straight lines). Again: We are
looking for good approximations of the regions ![]() by
rectangles.
by
rectangles.
The easiest way to choose a height for our rectangles is to choose the value of the function at the left (or right) end points of the small intervals [xi - 1, xi].
 |
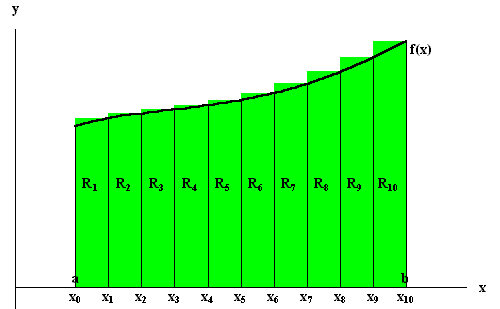 |
Let Li be the rectangle defined by the left-end point and
Ri be the rectangle defined by the right-end point. Then an
approximation to
Area(![]() ) is given by
) is given by
Example. Consider the function
Indeed if the function f (x) is not too badly behaved, we will
show that when n gets larger, the numbers LEFT(n) and
RIGHT(n) get closer to
Area(![]() ), i.e.
), i.e.
Note that in the expression
![]() f (x) dx the variable x
may be replaced by any other variable.
f (x) dx the variable x
may be replaced by any other variable.
Example. Let
![]()
![]() 0. Then we have
0. Then we have
Example. We have
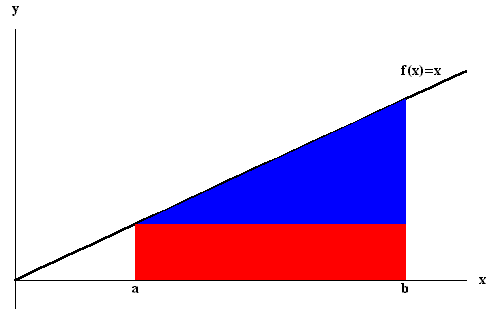 |
The rectangle (depicted in red) is bounded above by x = a and its
area is a(b - a). The triangle (in blue) is determined by the
points: (a, a), (a, b), and (b, b). Its area is
![]() (b - a)2. So we have
(b - a)2. So we have
A precise definition for the definite integral involves partitions and lower as well as upper sums:
Definition. A partition P of the interval [a, b] is a sequence of numbers {xi;i = 0, 1, ... , n} such that
For a function f (x) defined on [a, b] and a partition P of [a, b], set
Theorem. We have
This theorem is fundamental. Let us illustrate this with the following example.
Example. Use the above theorem to show
Exercise 1. Use similar ideas as used in the example above to show
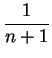 (bn + 1 - an + 1)
(bn + 1 - an + 1)
Exercise 2. Show that
Exercise 3. Consider the function
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.
![]()
![]()
![]()
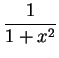 dx
dx ![]()
![]() .
.
![]()
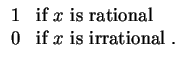
![]() f (x) dx does not exist.
f (x) dx does not exist.
 S.O.S MATHematics home page
S.O.S MATHematics home page
Helmut Knaust
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour