 Problems on Techniques of Integration
Problems on Techniques of Integration Problems on Techniques of Integration
Problems on Techniques of Integration

The logarithmic function is one of these functions whose derivative is very nice (rational function). So it is a good idea to use the integration by parts technique in which ![]() will be differentiated. There are basically two ways of doing this problem. You may try to find the antiderivative of
will be differentiated. There are basically two ways of doing this problem. You may try to find the antiderivative of ![]() then takes its values at
then takes its values at ![]() and
and ![]() . Or you may want to use the integration by parts for definite integrals.
. Or you may want to use the integration by parts for definite integrals.
Set
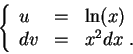
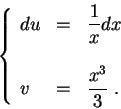
![\begin{displaymath}\int_1^e x^2 \ln(x) dx = \left[\frac{x^3}{3} \ln(x)\right]_1^...
...left[\frac{x^3}{3} \ln(x)\right]_1^e - \int_1^e \frac{x^2}{3}dx\end{displaymath}](img4.gif)
![\begin{displaymath}\int_1^e x^2 \ln(x) dx = \left[\frac{x^3}{3} \ln(x)\right]_1^...
..._1^e = \frac{e^3}{3} - \left(\frac{e^3}{9} - \frac{1}{9}\right)\end{displaymath}](img5.gif)
If you prefer to jump to the next problem, click on Next Problem below.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Mohamed A. Khamsi