Problems on Techniques of Integration

The trigonometric functions are nice functions since their derivatives and antiderivatives are easy to get. So for the integration by parts, these functions have the same behavior whether we differentiate them or take their antiderivatives. Therefore the focus should be on the other function involved in the integration. In this case, we must differentiate $f(x) = x^2$ because its derivative will lower its degree.

Set

$$\left\{\begin{array}{lll} u &=& x^2\\ dv &=& \sin(x) dx\;. \end{array}\right.$$

Then

$$\left\{\begin{array}{lll} du &=&2 x dx\\ v &=& -\cos(x)\;. \end{array}\right.$$

Since

$$\int u dv = u v - \int v du\;,$$

we get

$$\int x^2 \sin(x) dx = - x^2 \cos(x) + \int 2 x \cos(x) dx = - x^2 \cos(x) + 2 \int x \cos(x) dx\;.$$

In order to integrate the function $x \cos(x)$, we will need to do another integration by parts. This is very common that an integration by parts may lead to another one or may be more integration by parts. Set

$$\left\{\begin{array}{lll} u &=&x\\ dv &=& \cos(x)dx\;. \end{array}\right.$$

Then

$$\left\{\begin{array}{lll} du &=&dx\\ v &=& \sin(x)\;. \end{array}\right.$$

Since

$$\int u dv = u v - \int v du\;,$$

we get

$$\int x \cos(x) dx = x \sin(x) - \int \sin(x) dx = x \sin(x) + \cos(x)\;.$$

Hence

$$\int x^2 \sin(x) dx = - x^2 \cos(x) + x \sin(x) + \cos(x) + C\;.$$

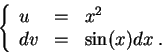
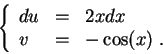
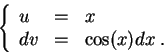
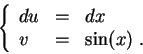
It is a common mistake to forget the constant $C$.

If you prefer to jump to the next problem, click on Next Problem below.

[Next Problem] [Matrix Algebra] [Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Complex Variables]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour