Problems on Techniques of Integration

We have a definite integral which depends on the integer $n=1,2,\cdots$ The fundamental formula $\sin^2(x) + \cos^2(x) = 1$ will be very useful. We have

$$\begin{array}{lll} I_{n+2} &=&\displaystyle \int_0^{\pi/2} \s... ...aystyle I_n - \int_0^{\pi/2}\sin^n(x)\cos^2(x)dx\\ \end{array}$$

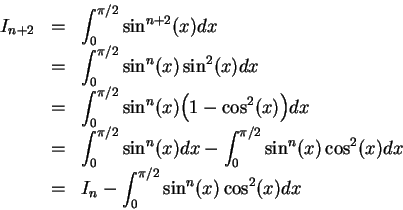
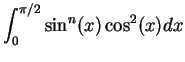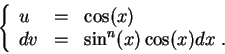
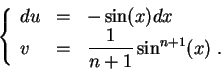
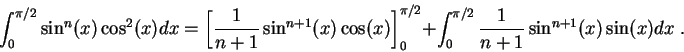
In order to evaluate $$\int_0^{\pi/2}\sin^n(x)\cos^2(x)dx$$, we will use the integration by parts technique. Since the derivative of $\sin^k(x)$ is $k \sin^{k-1}(x) \cos(x)$, we set

$$\left\{\begin{array}{lll} u &=& \cos(x)\\ dv &=& \sin^n(x)\cos(x) dx\;. \end{array}\right.$$

Then

$$\left\{\begin{array}{lll} du &=&-\sin(x)dx\\ v &=& \displaystyle \frac{1}{n+1} \sin^{n+1}(x)\;. \end{array}\right.$$

Since

$$\int_a^b u dv = [u v]_a^b - \int_a^b v du\;,$$

we get

$$\int_0^{\pi/2}\sin^n(x)\cos^2(x)dx = \left[\frac{1}{n+1} \sin... ...{\pi/2} + \int_0^{\pi/2}\frac{1}{n+1} \sin^{n+1}(x)\sin(x)dx\;.$$

Since $\sin(0) = 0$ and $\cos(\pi/2) = 0$, we get

$$\int_0^{\pi/2}\sin^n(x)\cos^2(x)dx = \frac{1}{n+1} \int_0^{\pi/2}\sin^{n+2}(x)dx = \frac{1}{n+1} I_{n+2}\;.$$

So

$$I_{n+2} = I_n - \int_0^{\pi/2}\sin^n(x)\cos^2(x)dx = I_n - \frac{1}{n+1} I_{n+2}$$

which implies

$$I_{n+2} = \frac{n+1}{n+2} I_n\;\cdot$$

This is the recurrent formula. In particular, the first integrals $I_0 = \pi/2$ and $I_1 = 1$, will give all the integrals $I_n$, for $n=1,2,\cdots$ For example, we have

$$I_2 = \frac{1}{2} I_0 = \frac{\pi}{4}\;\;\;\mbox{and}\;\; I_3 = \frac{2}{3}I_1 = \frac{2}{3}\;\cdot$$

If you prefer to jump to the next problem, click on Next Problem below.

[Next Problem] [Matrix Algebra] [Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Complex Variables]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour