 Problems on Techniques of Integration
Problems on Techniques of Integration

Use the Integration by Parts. Set
Then
So
In order to integrate the function
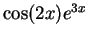 , we will need to do another integration by parts. Set
, we will need to do another integration by parts. Set
Then
So
Hence
which implies
or
Detailed Answer.
If you prefer to jump to the next problem, click on Next Problem
below.

[Next Problem]
[Matrix Algebra]
[Trigonometry]
[Calculus]
[Geometry]
[Algebra]
[Differential Equations]
[Complex Variables]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Mohamed A. Khamsi
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 Problems on Techniques of Integration
Problems on Techniques of Integration Problems on Techniques of Integration
Problems on Techniques of Integration
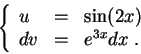

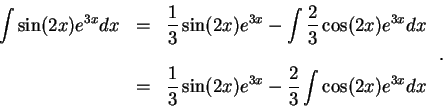
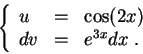
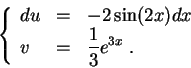
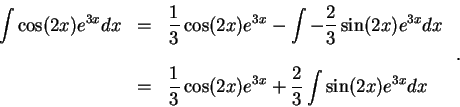

 S.O.S MATHematics home page
S.O.S MATHematics home page 