 Problems on Techniques of Integration
Problems on Techniques of Integration

We have
So
In order to integrate
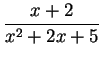 , we use the identity
, we use the identity
remembering the derivative of 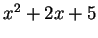 being
being 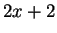 . So
. So
This implies
On one hand, we have
and also
We get
Detailed Answer.
If you prefer to jump to the next problem, click on Next Problem
below.

[Next Problem]
[Matrix Algebra]
[Trigonometry]
[Calculus]
[Geometry]
[Algebra]
[Differential Equations]
[Complex Variables]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Mohamed A. Khamsi
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 Problems on Techniques of Integration
Problems on Techniques of Integration Problems on Techniques of Integration
Problems on Techniques of Integration
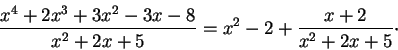
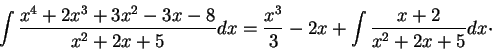
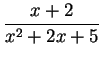 , we use the identity
, we use the identity
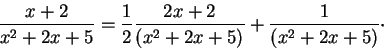
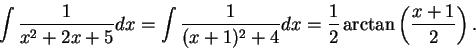

 S.O.S MATHematics home page
S.O.S MATHematics home page 