Problems on Techniques of Integration

The answer is given in any Table of integrals. Here we try to give the details for getting the answer.

By completing the square, we have

$$\begin{array}{lll} ax^2 + b x + c &=&\displaystyle a \left(x^... ...ac{b}{2a}\right)^2 + \frac{4ac - b^2}{4a^2} \right) \end{array}$$

Since $b^2 - 4a c < 0$, set

$$\omega = \frac{\sqrt{4ac - b^2}}{2a} \cdot$$

So

$$\int \frac{1}{ax^2 + b x + c}dx = \frac{1}{a} \int \frac{1}{\displaystyle \left(x + \frac{b}{2a}\right)^2 + \omega^2}dx\cdot$$

Hence

$$\int \frac{1}{ax^2 + b x + c}dx = \frac{1}{a \omega} \arctan\left(\frac{x + b/2a}{\omega}\right) + C$$

or

$$\int \frac{1}{ax^2 + b x + c}dx = \frac{2}{\sqrt{4ac - b^2}} \arctan\left(\frac{2a x + b}{\sqrt{4ac - b^2}}\right) + C .$$

It is a common mistake to forget the constant $C$.

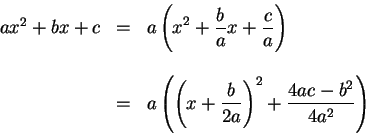
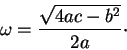
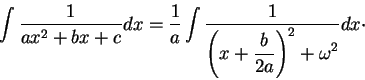
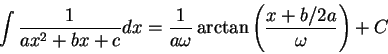
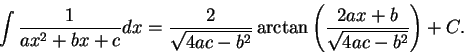
Remark. Recall the $\arctan$ formula

$$\int \frac{1}{x^2 + a^2} dx = \frac{1}{a} \arctan \left(\frac{x}{a}\right)$$

If you prefer to jump to the next problem, click on Next Problem below.

[Next Problem] [Matrix Algebra] [Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Complex Variables]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour